Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T14:00:54.839Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamical Zeta Function for Several Strictly Convex Obstacles

Published online by Cambridge University Press:  20 November 2018

Vesselin Petkov
Vesselin Petkov*
Affiliation:
Département de Mathématiques Appliquées, Université Bordeaux I, 351, Cours de la Libération, 33405 Talence, France e-mail: petkov@math.u-bordeaux1.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The behavior of the dynamical zeta function 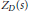${{Z}_{D}}(s)$ related to several strictly convex disjoint obstacles is similar to that of the inverse 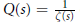$Q(s)\,=\,\frac{1}{\zeta (s)}$ of the Riemann zeta function 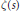$\zeta \left( s \right)$. Let 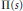$\prod \left( s \right)$ be the series obtained from 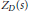${{Z}_{D}}(s)$ summing only over primitive periodic rays. In this paper we examine the analytic singularities of 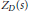${{Z}_{D}}(s)$ and 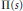$\prod \left( s \right)$ close to the line 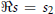$\Re s={{s}_{2}},$ where ${{s}_{2}}$ is the abscissa of absolute convergence of the series obtained by the second iterations of the primitive periodic rays. We show that at least one of the functions 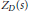${{Z}_{D}}(s),$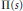$\prod \left( s \right)$ has a singularity at 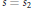$s\,=\,{{s}_{2}}$.

Keywords

11M3658J50dynamical zeta functionperiodic rays
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 1 , 01 March 2008 , pp. 100 - 113
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Bardos, C., Guillot, J. C. and Ralston, J., La relation de Poisson pour l’équation des ondes dans un ouvert non-borné. Comm. Partial Differantial Equations 7(1982), no. 8905–958.Google Scholar
[2] Burq, N., Controle de l’équation des plaques en présence d’obstacles strictement convexes. Suppl. Bull. Soc. Math. France, 121(1993), Mémoire 55.Google Scholar
[3] Cvitanović, P., Vattay, G. and Wirzba, A., Quantum fluids and classical determinants. In: Classical, Semiclassical and Quantum Dynamics in Atoms, Lecture Notes in Physics 487, Springer, Berlin, pp. 29–62.Google Scholar
[4] Dolgopyat, D., On decay of correlations of Anosov flows. Ann. of Math. 147(1998), no. 2, 357–390.Google Scholar
[5] Guillemin, V. and Melrose, R., The Poisson summation formula for manifolds with boundary. Adv. in Math. 32(1979), no. 3, 204–232.Google Scholar
[6] Ikawa, M., Decay of solutions of the wave equation in the exterior of several strictly convex bodies. Ann. Inst. Fourier (Grenoble), 38(1988), no. 2, 113–146.Google Scholar
[7] Ikawa, M., On the existence of poles of the scattering matrix for several convex bodies. Proc. Japan Acad. Ser. A Math. Sci. 64(1988), no. 4, 91–93.Google Scholar
[8] Ikawa, M., On the distribution of poles of the scattering matrix for several convex bodies. In: Functional-Analytic Methods for Partial Differential Equations, Lecture Notes in Math. 1450, Springer, Berlin, 1990, pp. 210–225.Google Scholar
[9] Ikawa, M., Singular perturbation of symbolic flows and poles of the zeta functions. Osaka J. Math. 27(1990), no. 2, 281–300; Addendum, Osaka J. Math. 29(1992), 161–174.Google Scholar
[10] Ikawa, M., On scattering by several convex bodies. J. Korean Math. Soc. 37(2000), no. 6, 991–1005.Google Scholar
[11] Lax, P. and Phillips, R., Scattering Theory, 2nd Edition, Pure and Applied Mathematics 26. Academic Press, New York, 1989.Google Scholar
[12] Lin, K. and Zworski, M., Quantum resonances in chaotic scattering. Chem. Phys. Lett. 355(2002), no. 1–2, 201–205.Google Scholar
[13] Melrose, R., Polynomial bound on the distribution of scattering poles. J. Funct. Anal. 53(1983), no. 3, 287–303.Google Scholar
[14] Morita, T., The symbolic representation of billiards without boundary condition. Trans. Amer. Math. Soc. 325(1991), no. 2, 819–828.Google Scholar
[15] Morita, T., Construction of K-stable foliations for two-dimensional dispersing billiards without eclipse. J. Math. Soc. Japan 56(2004), no. 3, 803–831.Google Scholar
[16] Naud, F., Analytic continuation of a dynamical zeta function under a Diophantine condition. Nonlinearity, 14(2001), no. 5, 995–1009.Google Scholar
[17] Parry, W. and Pollicot, M., Zeta functions and the periodic orbit structure of hyperbolic dynamics. Astérique, no. 187–188, 1990.Google Scholar
[18] Petkov, V., Analytic singularities of the dynamical zeta function. Nonlinearity, 12(1999), no. 6, 1663–1681.Google Scholar
[19] Petkov, V. and Stoyanov, L., Geometry of Reflecting Rays and Inverse Spectral Problems. Chichester, John Wiley, 1992.Google Scholar
[20] Sjöstrand, J., A trace formula and review of some estimates for resonances. In: Microlocal Analysis and Spectral Theory. NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci. 490, Kluwer, Dordrecht, 1997, 377–437.Google Scholar
[21] Sjöstrand, J. and Zworski, M., Lower bounds on the number of scattering poles. Comm. Partial Differential Equations 18(1993), no. 5–6, 847–857.Google Scholar
[22] Stoyanov, L., Exponential instability for a class of dispersing billiards. Ergodic Theory Dynam. Systems 19(1999), no. 1, 201–226.Google Scholar
[23] Stoyanov, L., Spectrum of the Ruelle operator and exponential decay of correlation flow for open billiard flows. Amer. J. Math. 123 (2001), 715–759.Google Scholar
[24] Stoyanov, L., Ruelle zeta functions and spectra of transfer operators for some Axiom A flows. Preprint. http://www.maths.uwa.edu.au/_stoyanov Google Scholar
[25] Stoyanov, L., Scattering resonances for several small convex bodies and the Lax-Phillips conjecture. To appear in Mem. Amer. Math. Soc. http://www.maths.uwa.edu.au/_stoyanov Google Scholar
[26] Stoyanov, L., Spectra of Ruelle transfer operators for contact flows on basic sets. Preprint, 2007. http://www.maths.uwa.edu.au/_stoyanov Google Scholar
[27] Vodev, G., Sharp bounds on the number of scattering poles for perturbations of the Laplacian. Comm. Math. Phys. 146(1992), no. 1, 205–216.Google Scholar
[28] Voros, A., Spectral functions, special functions and the Selberg zeta function. Commun. Math. Phys. 110(1987), no. 3, 437–465.Google Scholar
[29] Wirzba, A., Quantum mechanics and semi-classics of hyperbolic n-disk scattering systems. Phys. Rep. 309(1999), no. 1–2, 1–116.Google Scholar