Article contents
Dyson’s rank, overpartitions, and universal mock theta functions
Published online by Cambridge University Press: 07 September 2020
Abstract
In this paper, we decompose 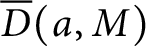 $\overline {D}(a,M)$ into modular and mock modular parts, so that it gives as a straightforward consequencethe celebrated results of Bringmann and Lovejoy on Maass forms. Let
$\overline {D}(a,M)$ into modular and mock modular parts, so that it gives as a straightforward consequencethe celebrated results of Bringmann and Lovejoy on Maass forms. Let 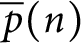 $\overline {p}(n)$ be the number of partitions of n and
$\overline {p}(n)$ be the number of partitions of n and 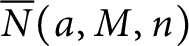 $\overline {N}(a,M,n)$ be the number of overpartitions of n with rank congruent to a modulo M. Motivated by Hickerson and Mortenson, we find and prove a general formula for Dyson’s ranks by considering the deviation of the ranks from the average:
$\overline {N}(a,M,n)$ be the number of overpartitions of n with rank congruent to a modulo M. Motivated by Hickerson and Mortenson, we find and prove a general formula for Dyson’s ranks by considering the deviation of the ranks from the average: 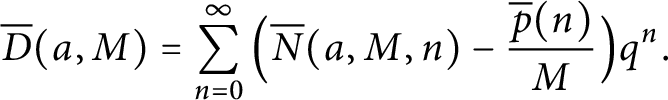
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
The author would like to thank the referees for their valuable comments and suggestions. This work was supported by the National Science Foundation of China (Grant Nos. 11871370 and 12001182) and the Fundamental Research Funds for the Central Universities (Grant No. 531118010411).
References
- 5
- Cited by


