Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T17:33:04.874Z Has data issue: false hasContentIssue false
  • English
  • Français

Embedding Coverings in Bundles

Published online by Cambridge University Press:  20 November 2018

Allan L. Edmonds
Allan L. Edmonds*
Affiliation:
Department of Mathematics Indiana University Bloomington, IN 47405 USA, email: edmonds@indiana.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 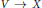$V\,\to \,X$ is a vector bundle of fiber dimension 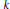$k$ and 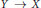$Y\,\to \,X$ is a finite sheeted covering map of degree 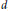$d$, the implications for the Euler class 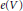$e(V)$ in 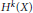${{H}^{k}}(X)$ of 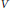$V$ implied by the existence of an embedding 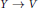$Y\,\to \,V$ lifting the covering map are explored. In particular it is proved that 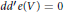$d{{d}^{\prime }}\text{e(V)}\text{=}\text{0}$ where 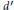${{d}^{\prime }}$ is a certain divisor of 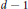$d\,-\,1$, and often 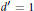${{d}^{\prime }}=1$.

Keywords

57M1055R2555S4057N35
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 1 , 01 March 1999 , pp. 52 - 55
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Bredon, Glen E., Introduction to Compact Transformation Groups. Academic Press, New York, 1972.Google Scholar
[2] Duvall, P. F. and Husch, L. S., Embedding finite covering spaces into bundles with applications. Topology Proc. 4 (1979), 361–370.Google Scholar
[3] Duvall, P. F. and Husch, L. S., Embedding coverings into bundles with applications. Mem. Amer.Math. Soc. 263, 1982.Google Scholar
[4] Hansen, Vagn Lundsgaard, Coverings defined by Weierstrass polynomials. J. Reine Angew. Math. 314 (1980), 29–39.Google Scholar
[5] Hansen, Vagn Lundsgaard, Embedding finite covering spaces into trivial bundles. Math. Ann. 236 (1978), 239–243.Google Scholar
[6] Mikhalkin, Grigory, Surfaces in the neighborhoods of other surfaces in smooth 4-manifolds. Proc. of the Gökova Geometry-Topology Conf. 1994, Scientific and Technical Research Council of Turkey, 1995, 82– 88; Turkish J. Math. 19 (1995), 201–206.Google Scholar
[7] Milnor, John W. and Stasheff, James D., Characteristic Classes. Ann. of Math. Stud. 76, Princeton Univ. Press, 1974.Google Scholar
[8] Zhang, Ping, On embeddings of smooth covering spaces in vector bundles. Topology Appl. 65 (1995), 21–27.Google Scholar