Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T16:42:54.511Z Has data issue: false hasContentIssue false
  • English
  • Français

Embeddings and Duality Theorems for Weak Classical Lorentz Spaces

Published online by Cambridge University Press:  20 November 2018

Amiran Gogatishvili  and
Luboš Pick
Amiran Gogatishvili
Affiliation:
Mathematical Institute, Czech Academy of Sciences, Žitná 25, 115 67 Praha 1, Czech Republic e-mail: gogatish@math.cas.cz
Luboš Pick
Affiliation:
Department of Mathematical Analysis, Faculty of Mathematics and Physics, Charles University, Sokolovská 83, 186 75 Praha, Czech Republic e-mail: pick@karlin.mff.cuni.cz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

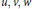We characterize the weight functions $u,v,w$ on 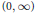$\left( 0,\infty \right)$ such that

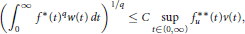$${{\left( \int\limits_{0}^{\infty }{{{f}^{*}}{{\left( t \right)}^{q}}w\left( t \right)}\,dt \right)}^{1/q}}\le C\,\,\underset{t\in \left( 0,\infty \right)}{\mathop{\sup }}\,{{f}_{u}}^{**}\left( t \right)v\left( t \right),$$

where

$${{f}_{u}}^{**}\left( t \right):={{\left( \int\limits_{0}^{t}{u\left( s \right)}\,ds \right)}^{-1}}\int\limits_{0}^{t}{{{f}^{*}}}\left( s \right)u\left( s \right)\,ds.$$

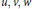As an application we present a new simple characterization of the associate space to the space ${{\Gamma }^{\infty }}\left( v \right)$, determined by the norm

$${{\left\| f \right\|}_{\Gamma \infty \left( v \right)}}=\,\underset{t\in \left( 0,\infty \right)}{\mathop{\sup }}\,{{f}^{**}}\left( t \right)v\left( t \right),$$

where

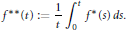$${{f}^{**}}\left( t \right):=\frac{1}{t}\int\limits_{0}^{t}{{{f}^{*}}}\left( s \right)\,ds.$$

Keywords

26D1046E20Discretizing sequenceantidiscretizationclassical Lorentz spacesweak Lorentz spacesembeddingsdualityHardy's inequality
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 1 , 01 March 2006 , pp. 82 - 95
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Bennett, C. and Sharpley, R., Interpolation of Operators. Pure and Applied Mathematics 129, Academic Press, Boston, 1988.Google Scholar
[2] Bradley, J. S., Hardy inequalities with mixed norms. Canad. Math. Bull. 49(1978), 405–408.Google Scholar
[3] Carro, M., García del Amo, A. and Soria, J., Weak-type weights and normable Lorentz spaces. Proc. Amer.Math. Soc. 49(1996), 849–857.Google Scholar
[4] Carro, M. and Soria, J., Weighted Lorentz spaces and the Hardy operator. J. Funct. Anal. 112(1993), 480–494.Google Scholar
[5] Carro, M. and Soria, J., Boundedness of some integral operators. Canad. J. Math. 45(1993), 1155–1166.Google Scholar
[6] Carro, M. and Soria, J., The Hardy-Littlewood maximal function and weighted Lorentz spaces. J. London Math. Soc. 49(1997), 146–158.Google Scholar
[7] Carro, M., Soria, J., Pick, L. and Stepanov, V., On embeddings between classical Lorentz spaces. Math. Inequal. Appl. 49(2001), 397–428.Google Scholar
[8] Gogatishvili, A. and Pick, L., Discretization and anti-discretization of rearrangement-invariant norms. Publ. Mat. 49(2003), 311–358.Google Scholar
[9] Gol’dman, M. L., On integral inequalities on a cone of functions with monotonicity properties. Soviet Math. Dokl. 44(1992), 581–587.Google Scholar
[10] Gol’dman, M. L., On integral inequalities on the set of functions with some properties of monotonicity. In: Function spaces, Differential Operators and Nonlinear Analysis, Teubner Texte Zur Math. 133, Teubner, Stuttgart, 1993, pp. 274–279.Google Scholar
[11] Gol’dman, M. L., Heinig, H. P. and Stepanov, V. D., On the principle of duality in Lorentz spaces. Canad. J. Math. 49(1996), 959–979.Google Scholar
[12] Grosse-Erdmann, K.-G., The Blocking Technique, Weighted Mean Operators and Hardy's Inequality. Lecture Notes in Mathematics 1679, Springer-Verlag, Berlin, 1998.Google Scholar
[13] Lorentz, G. G., On the theory of spaces Λ . Pacific J. Math. 49(1951), 411–429.Google Scholar
[14] Opic, B. and Kufner, A., Hardy-type inequalities. Pitman Research Notes in Mathematics 219, Longman Sci., Harlow, 1990.Google Scholar
[15] Sawyer, E., Boundedness of classical operators on classical Lorentz spaces. Studia Math. 49(1990), 145–158.Google Scholar
[16] Sinnamon, G., Spaces defined by level functions and their duals. Studia Math. 49(1994), 19–52.Google Scholar
[17] Sinnamon, G. and Stepanov, V. D., The weighted Hardy inequality: new proofs and the case p = 1 . J. London Math. Soc. 49(1996), 89–101.Google Scholar
[18] Stepanov, V. D., The weighted Hardy's inequality for nonincreasing functions. Trans. Amer. Math. Soc. 49(1993), 173–186.Google Scholar