Endomorphisms of the Quasi-Injective Hull of a Module

Extract

R is a ring and M is a right R-module for which R^l = {m ∊ M | mR = 0} is the zero submodule. Let and 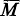be the injective hull and the quasi-injective hull of M respectively. Then 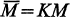where 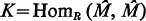[1]. The ring 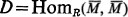plays an important role, in many cases, in the studying of R especially when D is a division ring. For x ∊ M, we denote the annihilator of x in R by x^γ = {r ∊ R | xr=0}, whereas x^γl={m ∊ M | mx^γ=0}. If N is a submodule of M and x ∊ M, x^-1(N) is the right ideal in R consisting of elements r in R where xr ∊ N.