Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-15T19:20:29.448Z Has data issue: false hasContentIssue false
  • English
  • Français

Equalizing the Coefficients in a Product of Polynomials

Published online by Cambridge University Press:  20 November 2018

R. A. Macleod  and
F. D. K. Roberts
R. A. Macleod
Affiliation:
University of Victoria, Victoria, British Columbia
F. D. K. Roberts
Affiliation:
University of Victoria, Victoria, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1959, Moser [4] posed the following problem: how should a pair of n-sided dice be loaded (identically) so that, on throwing the dice, the frequency of the most frequently occurring sum is as small as possible? This can be recast in the following form: determine for each n(≥1), the polynomial Pn(x) which minimizes the maximum coefficient in the polynomial 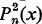subject to the conditions that the coefficients of Pn(x) are nonnegative and sum to unity.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 16 , Issue 4 , December 1973 , pp. 531 - 539
Copyright
Copyright © Canadian Mathematical Society 1973

References

1. Barrodale, I. and Roberts, F. D. K., Application of mathematical programming to lp approximation, in nonlinear programming, Rosen, Mangasarian and Ritter, eds., Academic Press, New York, (1970), 447–464.Google Scholar
2. Clements, G. F., On a min-max problem of Leo Moser, J. Combinatorial Theory, 4 (1968), 36–39.Google Scholar
3. Fröberg, C E., Introduction to numerical analysis, Addison-Wesley, Reading, Mass., 1969.Google Scholar
4. Moser, L., in Report of the Institute in the Theory of Numbers, University of Colorado, June 21-July 17 (1959), p. 342.Google Scholar
5. Moser, L., On the representation of 1, 2,…, n by sums, Acta Arith. VI (1960), 11–13.Google Scholar