No CrossRef data available.
Article contents
Equilateral Sets and a Schütte Theorem forthe 4-norm
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
A well-known theorem of Schütte (1963) gives a sharp lower bound for the ratio of the maximum and minimum distances between 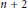 $n\,+\,2$ points in
$n\,+\,2$ points in  $n$ -dimensional Euclidean space. In this note we adapt Bárány’s elegant proof (1994) of this theorem to the space
$n$ -dimensional Euclidean space. In this note we adapt Bárány’s elegant proof (1994) of this theorem to the space 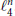 $\ell _{4}^{n}$ . This gives a new proof that the largest cardinality of an equilateral set in
$\ell _{4}^{n}$ . This gives a new proof that the largest cardinality of an equilateral set in 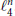 $\ell _{4}^{n}$ is
$\ell _{4}^{n}$ is 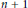 $n\,+\,1$ and gives a constructive bound for an interval
$n\,+\,1$ and gives a constructive bound for an interval  $\left( 4\,-\,{{\varepsilon }_{n}},\,4\,+\,{{\varepsilon }_{n}} \right)$ of values of
$\left( 4\,-\,{{\varepsilon }_{n}},\,4\,+\,{{\varepsilon }_{n}} \right)$ of values of 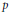 $p$ close to 4 for which it is known that the largest cardinality of an equilateral set in
$p$ close to 4 for which it is known that the largest cardinality of an equilateral set in 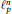 $\ell _{p}^{n}$ is
$\ell _{p}^{n}$ is 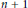 $n\,+\,1$ .
$n\,+\,1$ .
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2014
References
[1]
Alon, N. and Pudlák, P., Equilateral sets in ln p. Geom. Funct. Anal.
13 (2003), no. 3, 467–482. http://dx.doi.org/10.1007/s00039-003-0418-7
Google Scholar
[2]
Bárány, I., The densest (n + 2)-set in Rn. In: Intuitive geometry (Szeged, 1991), Coll. Math. Soc. János Bolyai, 63, North-Holland, Amsterdam, 1994, pp. 7–10.Google Scholar
[3]
Barvinok, A., A course in convexity. Graduate Studies in Mathematics, 54, American Mathematical Society, Providence, RI, 2002.Google Scholar
[4]
Guy, R. K., Unsolved problems: An olla-podrida of open problems, often oddly posed. Amer. Math. Monthly
90 (1983), no. 3, 196–199. http://dx.doi.org/10.2307/2975549
Google Scholar
[5]
Schoenberg, I. J., Linkages and distance geometry. II. On sets of n + 2 points in En that are most nearly equilateral. Indag. Math.
31 (1969), 53–63.Google Scholar
[6]
Schütte, K., Minimale Durchmesser endlicher Punktmengen mit vorgeschriebenem Mindestabstand. Math. Ann.
150 (1963), 91–98. http://dx.doi.org/10.1007/BF01396584
Google Scholar
[8]
Smyth, C., Equilateral sets in d p. In: Thirty essays on geometric graph theory, Springer, New York, 2013. pp. 483–488.Google Scholar
[9]
Swanepoel, K. J., A problem of Kusner on equilateral sets. Arch. Math. (Basel)
83 (2004), no. 2, 164–170.Google Scholar

