No CrossRef data available.
Published online by Cambridge University Press: 20 August 2020
A set
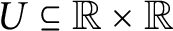 $U \subseteq {\mathbb {R}} \times {\mathbb {R}}$
is universal for countable subsets of
$U \subseteq {\mathbb {R}} \times {\mathbb {R}}$
is universal for countable subsets of
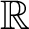 ${\mathbb {R}}$
if and only if for all
${\mathbb {R}}$
if and only if for all
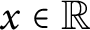 $x \in {\mathbb {R}}$
, the section
$x \in {\mathbb {R}}$
, the section
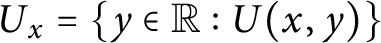 $U_x = \{y \in {\mathbb {R}} : U(x,y)\}$
is countable and for all countable sets
$U_x = \{y \in {\mathbb {R}} : U(x,y)\}$
is countable and for all countable sets
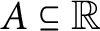 $A \subseteq {\mathbb {R}}$
, there is an
$A \subseteq {\mathbb {R}}$
, there is an
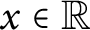 $x \in {\mathbb {R}}$
so that
$x \in {\mathbb {R}}$
so that
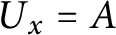 $U_x = A$
. Define the equivalence relation
$U_x = A$
. Define the equivalence relation
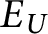 $E_U$
on
$E_U$
on
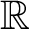 ${\mathbb {R}}$
by
${\mathbb {R}}$
by
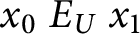 $x_0 \ E_U \ x_1$
if and only if
$x_0 \ E_U \ x_1$
if and only if
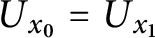 $U_{x_0} = U_{x_1}$
, which is the equivalence of codes for countable sets of reals according to U. The Friedman–Stanley jump,
$U_{x_0} = U_{x_1}$
, which is the equivalence of codes for countable sets of reals according to U. The Friedman–Stanley jump,
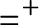 $=^+$
, of the equality relation takes the form
$=^+$
, of the equality relation takes the form
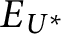 $E_{U^*}$
where
$E_{U^*}$
where
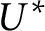 $U^*$
is the most natural Borel set that is universal for countable sets. The main result is that
$U^*$
is the most natural Borel set that is universal for countable sets. The main result is that
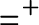 $=^+$
and
$=^+$
and
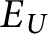 $E_U$
for any U that is Borel and universal for countable sets are equivalent up to Borel bireducibility. For all U that are Borel and universal for countable sets,
$E_U$
for any U that is Borel and universal for countable sets are equivalent up to Borel bireducibility. For all U that are Borel and universal for countable sets,
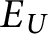 $E_U$
is Borel bireducible to
$E_U$
is Borel bireducible to
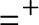 $=^+$
. If one assumes a particular instance of
$=^+$
. If one assumes a particular instance of
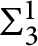 $\mathbf {\Sigma }_3^1$
-generic absoluteness, then for all
$\mathbf {\Sigma }_3^1$
-generic absoluteness, then for all
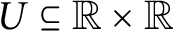 $U \subseteq {\mathbb {R}} \times {\mathbb {R}}$
that are
$U \subseteq {\mathbb {R}} \times {\mathbb {R}}$
that are
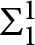 $\mathbf {\Sigma }_1^1$
(continuous images of Borel sets) and universal for countable sets, there is a Borel reduction of
$\mathbf {\Sigma }_1^1$
(continuous images of Borel sets) and universal for countable sets, there is a Borel reduction of
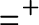 $=^+$
into
$=^+$
into
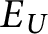 $E_U$
.
$E_U$
.
The author was supported by NSF grant DMS-1703708.