Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T03:40:42.998Z Has data issue: false hasContentIssue false
  • English
  • Français

Erratum: The Duality Problem For The Class of AM-Compact Operators On Banach Lattices

Published online by Cambridge University Press:  20 November 2018

Belmesnaoui Aqzzouz
Belmesnaoui Aqzzouz*
Affiliation:
Université Mohammed V-Souissi, Faculté des Sciences Économiques Juridiques et Sociales, Département d’ Économie, B. P. 5295 SalaEljadida, Moroccoe-mail: baqzzouz@hotmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is proved that if a positive operator 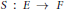$S\,:\,E\,\to \,F$ is 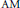$\text{AM}$-compact whenever its adjoint 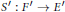${{S}^{'}}:{{F}^{'}}\to {{E}^{'}}$ is 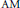$\text{AM}$-compact, then either the norm of $\text{F}$ is order continuous or 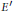$E\prime $ is discrete.

Keywords

46A4046B4046B42
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 4 , 01 December 2011 , pp. 577 - 579
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Aliprantis, C. D. and Burkinshaw, O., Locally solid Riesz spaces. Pure and Applied Mathematics, 76, Academic Press, New York-London, 1978.Google Scholar
[2] Aliprantis, C. D. and Burkinshaw, O., Positive operators. Reprint of the 1985 original, Springer, Dordrecht, 2006.Google Scholar
[3] Aqzzouz, B., Nouira, R., and Zraoula, L., The duality problem for the class of AM-compact operators on Banach lattices. Canad. Math. Bull. 51(2008), no. 1, 15–20. doi:10.4153/CMB-2008-002-0Google Scholar
[4] Aqzzouz, B., Elbour, A., and Hmichane, J., The duality problem for the class of b-weakly compact operators. Positivity 13(2009), no. 4, 683–692. doi:10.1007/s11117-008-2288-6Google Scholar
[5] Chen, Z. L. and Wickstead, A. W., Some applications of Rademacher sequences in Banach lattices. Positivity 2(1998), no. 2, 171–191. doi:10.1023/A:1009767118180Google Scholar
[6] Meyer-Nieberg, P., Banach lattices. Universitext, Springer-Verlag, Berlin, 1991.Google Scholar
[7] Wnuk, W., Banach lattices with order continuous norms. Polish Scientific Publishers, Warsaw, 1999.Google Scholar
[8] Zaanen, A. C., Riesz spaces. II. North-Holland Mathematical Library, 30, North-Holland Publishing Co., Amsterdam, 1983.Google Scholar