Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T22:08:02.479Z Has data issue: false hasContentIssue false
  • English
  • Français

Essential Commutants of Semicrossed Products

Published online by Cambridge University Press:  20 November 2018

Kei Hasegawa
Kei Hasegawa*
Affiliation:
Graduate School of Mathematics, Kyushu University, Fukuoka 819-0395, Japan. e-mail: ma213034@math.kyushu-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 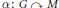$\alpha :\,G\,\curvearrowright \,M$ be a spatial action of a countable abelian group on a “spatial” von Neumann algebra 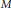$M$ and let $S$ be its unital subsemigroup with 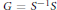$G\,=\,{{S}^{-1}}S$. We explicitly compute the essential commutant and the essential fixed-points, modulo the Schatten 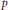$p$-class or the compact operators, of the 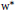${{w}^{*}}$-semicrossed product of 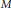$M$ by $S$ when 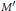${{M}^{'}}$ contains no non-zero compact operators. We also prove a weaker result when 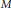$M$ is a von Neumann algebra on a finite dimensional Hilbert space and 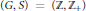$\left( G,\,S \right)\,=\,\left( \mathbb{Z},\,{{\mathbb{Z}}_{+}} \right)$, which extends a famous result due to Davidson (1977) for the classical analytic Toeplitz operators.

Keywords

47L6547A55essential commutantsemicrossed product
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 1 , 01 March 2015 , pp. 91 - 104
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Brown, A. and Halmos, P. R., Algebraic properties of Toeplitz operators. J. Reine Angew. Math. 213(1963/1964), 89–102. Google Scholar
[2] Davidson, K. R., On operators commuting with Toeplitz operators modulo the compact operators. J. Funct. Anal. 24 (1977), 291–302. http://dx.doi.org/10.1016/0022-1236(77)90060-X Google Scholar
[3] Douglas, R. G., Banach algebra techniques in operator theory. Second ed., Graduate Texts in Mathematics, 179, Springer-Verlag, New York, 1998.Google Scholar
[4] Haagerup, U., The standard form of von Neumann algebras. Math. Scand. 37 (1975), no. 2, 271–283. Google Scholar
[5] Hewiit, E. and Ross, K. A., Abstract harmonic analysis. Vol. I. Second ed., Grundlehren der MathematischenWissensrhaften, 115, Springer-Verlag, Berlin-New York, 1979.Google Scholar
[6] Hiai, F., Log-majorizations and norm inequalities for exponential operators. In: Linear Operators. Banach Center Publ., 38, Polish Acad. Sci., Warsaw, 1997, pp. 119–181..Google Scholar
[7] Hoover, T.B., Derivations, homomorphisms, and operator ideals. Proc. Amer. Math. Soc. 62 (1977), no. 2, 293–298. http://dx.doi.org/10.1090/S0002-9939-1977-0435860-9 Google Scholar
[8] Johnson, B. E. and Parrott, S. K., Operators commuting with a von Neumann algebra modulo the set of compact operators. J. Funct. Anal. 11 (1972), 39–61. http://dx.doi.org/10.1016/0022-1236(72)90078-X Google Scholar
[9] Kakariadis, E., Semicrossed products and reflexivity. J. Operator Theory 67 (2012), no. 2, 379–395. Google Scholar
[10] Loebl, R.I. and Muhly, P.S., Analyticity and flows in von Neumann algebras. J. Funct. Anal. 29 (1978), no. 2, 214–252. http://dx.doi.org/10.1016/0022-1236(78)90007-1 Google Scholar
[11] McAsey, M., Muhly, P. S., and Saito, K-S., Nonselfadjoint crossed products (invariant subspaces and maximality). Trans. Amer. Math. Soc. 248 (1979), no. 2, 381–409. http://dx.doi.org/10.1090/S0002-9947-1979-0522266-3 Google Scholar
[12] Muhly, P. S. and J. Xia, On automorphisms of the Toeplitz algebra. Amer. J. Math. 122 (2000), no. 6, 1121–1138. http://dx.doi.org/10.1353/ajm.2000.0047 Google Scholar
[13] Popa, S., The commutant modulo the set of compact operators of a von Neumann algebra. J. Funct. Anal. 71 (1987), no. 2, 393–408. http://dx.doi.org/10.1016/0022-1236(87)90011-5 Google Scholar
[14] Saito, K-S., Toeplitz operators associated with analytic crossed products. Math. Proc. Cambridge Philos. Soc. 108 (1990), no. 3, 539–549. http://dx.doi.org/10.1017/S0305004100069425 Google Scholar
[15] Takesaki, M., Theory of operator algebras. II. Encyclopaedia of Mathematical Sciences, 125. Operator Algebras and Non-commutative Geometry, 6, Springer-Verlag, Berlin, 2003.Google Scholar
[16] Xia, J., A characterization of compact perturbations of Toeplitz operators. Trans. Amer. Math. Soc. 361 (2009), no. 10, 5163–5175. http://dx.doi.org/10.1090/S0002-9947-09-04736-9 Google Scholar