Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-27T23:33:25.827Z Has data issue: false hasContentIssue false
  • English
  • Français

Essential Dimension, Symbol Length and 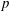$p$-rank

Part of: Linear algebraic groups and related topics Higher algebraic $K$-theory Division rings and semisimple Artin rings General commutative ring theory

Published online by Cambridge University Press:  04 February 2020

Adam Chapman  and
Kelly McKinnie
Adam Chapman
Affiliation:
Department of Computer Science, Tel-Hai College, Upper Galilee, 12208, Israel Email: adam1chapman@yahoo.com
Kelly McKinnie
Affiliation:
Department of Mathematical Sciences, University of Montana, Missoula, MT 59812, USA Email: kelly.mckinnie@mso.umt.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that the essential dimension of central simple algebras of degree 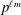$p^{\ell m}$ and exponent 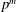$p^{m}$ over fields 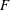$F$ containing a base-field 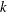$k$ of characteristic 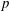$p$ is at least 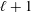$\ell +1$ when 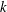$k$ is perfect. We do this by observing that the 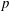$p$-rank of 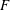$F$ bounds the symbol length in 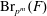$\text{Br}_{p^{m}}(F)$ and that there exist indecomposable 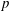$p$-algebras of degree 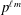$p^{\ell m}$ and exponent 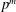$p^{m}$. We also prove that the symbol length of the Kato-Milne cohomology group 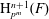$\text{H}_{p^{m}}^{n+1}(F)$ is bounded from above by 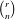$\binom{r}{n}$ where $r$ is the 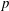$p$-rank of the field, and provide upper and lower bounds for the essential dimension of Brauer classes of a given symbol length.

Keywords

essential dimensionsymbol lengthp-rankfields of positive characteristicBrauer groupcentral simple algebraKato–Milne cohomology

MSC classification

Primary: 16K20: Finite-dimensional
Secondary: 13A35: Characteristic $p$ methods (Frobenius endomorphism) and reduction to characteristic $p$; tight closure 19D45: Higher symbols, Milnor $K$-theory 20G10: Cohomology theory
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 4 , December 2020 , pp. 882 - 890
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aravire, R., Jacob, B., and O’Ryan, M., The de Rham Witt complex, cohomological kernels and p m-extensions in characteristic p. J. Pure Appl. Algebra 222(2018), 3891–3945. https://doi.org/10.1016/j.jpaa.2018.02.013CrossRefGoogle Scholar
Albert, A., Structure of algebras. Colloquium Publications, 24, American Mathematical Society, Providence, RI, 1968.Google Scholar
Baek, S., Essential dimension of simple algebras in positive characteristic. C. R. Math. Acad. Sci. Paris 349(2011), no. 7–8, 375–378. https://doi.org/10.1016/j.crma.2011.03.014CrossRefGoogle Scholar
Baek, S. and Merkurjev, A., Invariants of simple algebras. Manuscripta Math. 129(2009), no. 4, 409–421. https://doi.org/10.1007/s00229-009-0265-4CrossRefGoogle Scholar
Baek, S. and Merkurjev, A., Essential dimension of central simple algebras. Acta Math. 209(2012), no. 1, 1–27. https://doi.org/10.1007/s11511-012-0080-8CrossRefGoogle Scholar
Bourbaki, N., Algebra. II. Chapters 4–7. Elements of Mathematics (Berlin), Translated from the French by P. M. Cohn and J. Howie, Springer-Verlag, Berlin, 1990.Google Scholar
Chapman, A. and McKinnie, K., Kato–Milne cohomology and polynomial forms. J. Pure Appl. Algebra 222(2018), 3547–3559. https://doi.org/10.1016/j.jpaa.2017.12.022CrossRefGoogle Scholar
Chapman, A. and McKinnie, K., The u n-invariant and the symbol length of H 2n(F). Proc. Amer. Math. Soc. 147(2019), 513–521. https://doi.org/10.1090/proc/14308CrossRefGoogle Scholar
Florence, M., On the symbol length of p-algebras. Compos. Math. 149(2013), 1353–1363. https://doi.org/10.1112/S0010437X13007070CrossRefGoogle Scholar
Gille, P. and Szamuely, T., Central simple algebras and Galois cohomology. Cambridge Studies in Advanced Mathematics, 165, Cambridge University Press, Cambridge, 2017.CrossRefGoogle Scholar
Izhboldin, O. T., On the cohomology groups of the field of rational functions. In: Mathematics in St. Petersburg, Amer. Math. Soc. Transl. Ser. 2, 174, American Mathematical Society, Providence, RI, 1996, pp. 21–44. https://doi.org/10.1090/trans2/174/03Google Scholar
Izhboldin, O., p-primary part of the Milnor K-groups and Galois cohomologies of fields of characteristic p. In: Invitation to higher local fields (Münster, 1999), Geom. Topol. Monogr., 3, Geom. Topol. Publ., Coventry, 2000, pp. 19–41. https://doi.org/10.2140/gtm.2000.3.19Google Scholar
Jacobson, N., Basic algebra. II. Second ed., W. H. Freeman and Company, New York, 1989.Google Scholar
Karpenko, N. A., Torsion in CH2of Severi–Brauer varieties and indecomposability of generic algebras. Manuscripta Math. 88(1995), 109–117. https://doi.org/10.1007/BF02567809CrossRefGoogle Scholar
Karpenko, N. A., Codimension 2 cycles on Severi–Brauer varieties. K-Theory 13(1998), 305–330. https://doi.org/10.1023/A:1007705720373CrossRefGoogle Scholar
Ledet, A., On the essential dimension of p-groups. In: Galois theory and modular forms, Dev. Math., 11, Kluwer Acad. Publ., Boston, MA, 2004, pp. 159–172. https://doi.org/10.1007/978-1-4613-0249-0_8CrossRefGoogle Scholar
Matzri, E., Symbol length in the Brauer group of a field. Trans. Amer. Math. Soc. 368(2016), 413–427. https://doi.org/10.1090/tran/6326CrossRefGoogle Scholar
McKinnie, K., Indecomposable p-algebras and Galois subfields in generic abelian crossed products. J. Algebra 320(2008), 1887–1907. https://doi.org/10.1016/j.jalgebra.2008.05.028CrossRefGoogle Scholar
McKinnie, K., Essential dimension of generic symbols in characteristic p. Forum Math. Sigma 5(2017), e14, 30. https://doi.org/10.1017/fms.2017.11CrossRefGoogle Scholar
Merkurjev, A. S., Essential dimension: a survey. Transform. Groups 18(2013), 415–481. https://doi.org/10.1007/s00031-013-9216-yCrossRefGoogle Scholar
Mammone, P. and Merkurjev, A., On the corestriction of p n-symbol. Israel J. Math. 76(1991), 73–79. https://doi.org/10.1007/BF02782844CrossRefGoogle Scholar
Mammone, P., Tignol, J.-P., and Wadsworth, A., Fields of characteristic 2 with prescribed u-invariants. Math. Ann. 290(1991), 109–128. https://doi.org/10.1007/BF01459240CrossRefGoogle Scholar
Rowen, L. H., Division algebras of exponent 2 and characteristic 2. J. Algebra 90(1984), 71–83. https://doi.org/10.1016/0021-8693(84)90199-6CrossRefGoogle Scholar