Article contents
Estimates for generalized Bohr radii in one and higher dimensions
Published online by Cambridge University Press: 04 November 2022
Abstract
In this article, we study a generalized Bohr radius 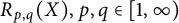 $R_{p, q}(X), p, q\in [1, \infty )$ defined for a complex Banach space X. In particular, we determine the exact value of
$R_{p, q}(X), p, q\in [1, \infty )$ defined for a complex Banach space X. In particular, we determine the exact value of 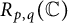 $R_{p, q}(\mathbb {C})$ for the cases (i)
$R_{p, q}(\mathbb {C})$ for the cases (i) 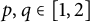 $p, q\in [1, 2]$, (ii)
$p, q\in [1, 2]$, (ii) 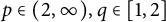 $p\in (2, \infty ), q\in [1, 2]$, and (iii)
$p\in (2, \infty ), q\in [1, 2]$, and (iii) 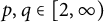 $p, q\in [2, \infty )$. Moreover, we consider an n-variable version
$p, q\in [2, \infty )$. Moreover, we consider an n-variable version 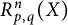 $R_{p, q}^n(X)$ of the quantity
$R_{p, q}^n(X)$ of the quantity 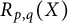 $R_{p, q}(X)$ and determine (i)
$R_{p, q}(X)$ and determine (i) 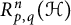 $R_{p, q}^n(\mathcal {H})$ for an infinite-dimensional complex Hilbert space
$R_{p, q}^n(\mathcal {H})$ for an infinite-dimensional complex Hilbert space 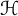 $\mathcal {H}$ and (ii) the precise asymptotic value of
$\mathcal {H}$ and (ii) the precise asymptotic value of 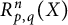 $R_{p, q}^n(X)$ as
$R_{p, q}^n(X)$ as 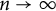 $n\to \infty $ for finite-dimensional X. We also study the multidimensional analog of a related concept called the p-Bohr radius. To be specific, we obtain the asymptotic value of the n-dimensional p-Bohr radius for bounded complex-valued functions, and in the vector-valued case, we provide a lower estimate for the same, which is independent of n.
$n\to \infty $ for finite-dimensional X. We also study the multidimensional analog of a related concept called the p-Bohr radius. To be specific, we obtain the asymptotic value of the n-dimensional p-Bohr radius for bounded complex-valued functions, and in the vector-valued case, we provide a lower estimate for the same, which is independent of n.
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
The author of this article is supported by a Research Associateship provided by the Stat-Math Unit of ISI Kolkata.
References
- 4
- Cited by


