Exact Filling of Figures with the Derivatives of Smooth Mappings Between Banach Spaces

Abstract

We establish sufficient conditions on the shape of a set 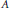$A$ included in the space 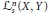$\mathcal{L}_{s}^{n}\left( X,Y \right)$ of the $n$-linear symmetric mappings between Banach spaces 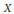$X$ and $Y$ , to ensure the existence of a 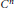${{C}^{n}}$-smooth mapping 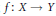$f:X\to Y$, with bounded support, and such that 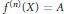${{f}^{\left( n \right)}}\left( X \right)=A$, provided that 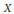$X$ admits a 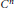${{C}^{n}}$-smooth bump with bounded $n$-th derivative and dens 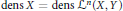$\text{dens }X=\text{dens }{{\mathcal{L}}^{n}}\left( X,Y \right)$. For instance, when 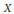$X$ is infinite-dimensional, every bounded connected and open set 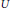$U$ containing the origin is the range of the $n$-th derivative of such amapping. The same holds true for the closure of 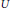$U$, provided that every point in the boundary of 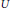$U$ is the end point of a path within 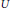$U$. In the finite-dimensional case, more restrictive conditions are required. We also study the Fréchet smooth case for mappings from 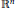${{\mathbb{R}}^{n}}$ to a separable infinite-dimensional Banach space and the Gâteaux smooth case for mappings defined on a separable infinite-dimensional Banach space and with values in a separable Banach space.