No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Let 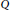 $Q$
be a finite acyclic quiver, let
$Q$
be a finite acyclic quiver, let 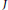 $J$
be an ideal of
$J$
be an ideal of 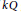 $kQ$
generated by all arrows in
$kQ$
generated by all arrows in 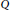 $Q$, and let
$Q$, and let 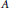 $A$
be a finite-dimensional
$A$
be a finite-dimensional  $k$
-algebra. The category of all finite-dimensional representations of
$k$
-algebra. The category of all finite-dimensional representations of 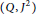 $\left( Q,\,{{J}^{2}} \right)$
over
$\left( Q,\,{{J}^{2}} \right)$
over 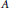 $A$ is denoted by
$A$ is denoted by 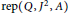 $\text{rep}\left( Q,\,{{J}^{2}},\,A \right)$
. In this paper, we introduce the category
$\text{rep}\left( Q,\,{{J}^{2}},\,A \right)$
. In this paper, we introduce the category 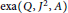 $\text{exa}\left( Q,{{J}^{2}},A \right),$
which is a subcategory of
$\text{exa}\left( Q,{{J}^{2}},A \right),$
which is a subcategory of 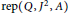 $\text{rep}\left( Q,\,{{J}^{2}},\,A \right)$ of all exact representations. The main result of this paper explicitly describes the Gorenstein-projective representations in
$\text{rep}\left( Q,\,{{J}^{2}},\,A \right)$ of all exact representations. The main result of this paper explicitly describes the Gorenstein-projective representations in 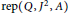 $\text{rep}\left( Q,\,{{J}^{2}},\,A \right)$, via the exact representations plus an extra condition. As a corollary,
$\text{rep}\left( Q,\,{{J}^{2}},\,A \right)$, via the exact representations plus an extra condition. As a corollary, 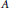 $A$ is a self-injective algebra if and only if the Gorenstein-projective representations are exactly the exact representations of
$A$ is a self-injective algebra if and only if the Gorenstein-projective representations are exactly the exact representations of 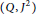 $\left( Q,\,{{J}^{2}} \right)$ over
$\left( Q,\,{{J}^{2}} \right)$ over 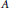 $A$.
$A$.