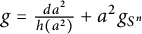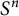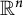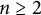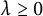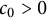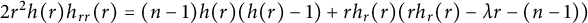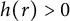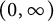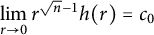1 Introduction
Ricci flow is an important technique in geometry and has a lot of applications in geometry [Reference Kleiner and Lott10, Reference Morgan and Tian12, Reference Perelman14, Reference Perelman15]. For example, recently, Perelman [Reference Perelman14, Reference Perelman15] used Ricci flow to prove the Poincaré conjecture. In the study of Ricci flow, one is interested to study the Ricci solitons which are self-similar solutions of Ricci flow. On the other hand, by a limiting argument, the behavior of the Ricci flow near the singular time is usually similar to the behavior of Ricci solitons.
Hence, in order to understand Ricci flow, it is important to study the Ricci solitons. In [Reference Brendle3], Brendle used singular rotationally symmetric steady solitons to construct barrier functions which plays an important role in the proof there that confirms a conjecture of Perelman on three-dimensional ancient
![]() $\kappa $
solution to the Ricci flow. We refer the reader to the papers by Alexakis, Chen, and Fournodavlos [Reference Alexakis, Chen and Fournodavlos1], Brendle [Reference Brendle2], Bryant [Reference Bryant4], Cao and Zhou [Reference Cao, Lee, Lin and Tsui5, Reference Cao and Zhou6], Feldman, Ilmanen, and Knopf [Reference Feldman, Ilmanen and Knopf8], Hsu [Reference Hsu9], Li and Wang [Reference Li and Wang11], Munteanu and Sesum [Reference Munteanu and Sesum13], Petersen and Wylie [Reference Petersen and Wylie16], and so forth and the book [Reference Chow, Chu, Glickenstein, Guenther, Isenberg, Ivey, Knopf, Lu, Luo and Ni7] by Chow et al. for some recent results on Ricci solitons.
$\kappa $
solution to the Ricci flow. We refer the reader to the papers by Alexakis, Chen, and Fournodavlos [Reference Alexakis, Chen and Fournodavlos1], Brendle [Reference Brendle2], Bryant [Reference Bryant4], Cao and Zhou [Reference Cao, Lee, Lin and Tsui5, Reference Cao and Zhou6], Feldman, Ilmanen, and Knopf [Reference Feldman, Ilmanen and Knopf8], Hsu [Reference Hsu9], Li and Wang [Reference Li and Wang11], Munteanu and Sesum [Reference Munteanu and Sesum13], Petersen and Wylie [Reference Petersen and Wylie16], and so forth and the book [Reference Chow, Chu, Glickenstein, Guenther, Isenberg, Ivey, Knopf, Lu, Luo and Ni7] by Chow et al. for some recent results on Ricci solitons.
We say that a Riemannian metric
![]() $g=(g_{ij})$
on a Riemannian manifold M is a gradient Ricci soliton if there exist a smooth function f on M and a constant
$g=(g_{ij})$
on a Riemannian manifold M is a gradient Ricci soliton if there exist a smooth function f on M and a constant
![]() $\lambda \in \mathbb {R}$
such that the Ricci curvature
$\lambda \in \mathbb {R}$
such that the Ricci curvature
![]() $R_{ij}$
of the metric g satisfies
$R_{ij}$
of the metric g satisfies
The gradient soliton is called an expanding gradient Ricci soliton if
![]() $\lambda>0$
. It is called a steady gradient Ricci soliton if
$\lambda>0$
. It is called a steady gradient Ricci soliton if
![]() $\lambda =0$
and it is called a shrinking gradient Ricci soliton if
$\lambda =0$
and it is called a shrinking gradient Ricci soliton if
![]() $\lambda <0$
.
$\lambda <0$
.
Existence of rotationally symmetric steady and expanding three-dimensional gradient Ricci solitons were proved by Bryant [Reference Bryant4] using the phase method and by Hsu [Reference Hsu9] using fixed-point argument. On the other hand, as observed by Bryant [Reference Bryant4] for
![]() $n=2$
and Chow et al. (cf. Lemma 1.21 and Section 4 of Chapter 1 of [Reference Chow, Chu, Glickenstein, Guenther, Isenberg, Ivey, Knopf, Lu, Luo and Ni7]) for
$n=2$
and Chow et al. (cf. Lemma 1.21 and Section 4 of Chapter 1 of [Reference Chow, Chu, Glickenstein, Guenther, Isenberg, Ivey, Knopf, Lu, Luo and Ni7]) for
![]() $n\ge 2$
, for any
$n\ge 2$
, for any
![]() $n\ge 2$
, if
$n\ge 2$
, if
![]() $(M,g)$
is an
$(M,g)$
is an
![]() $(n+1)$
-dimensional rotational symmetric gradient Ricci soliton which satisfies (1.1) for some smooth function f and constant
$(n+1)$
-dimensional rotational symmetric gradient Ricci soliton which satisfies (1.1) for some smooth function f and constant
![]() $\lambda \in \mathbb {R}$
with
$\lambda \in \mathbb {R}$
with
where
![]() $g_{S^n}$
is the standard metric on the unit sphere
$g_{S^n}$
is the standard metric on the unit sphere
![]() $S^n$
in
$S^n$
in
![]() $\mathbb {R}^n$
, then the Ricci curvature of g is given by
$\mathbb {R}^n$
, then the Ricci curvature of g is given by
and
Hence, by (1.1), (1.3), and (1.4) (cf. [Reference Alexakis, Chen and Fournodavlos1, Reference Bryant4, Reference Chow, Chu, Glickenstein, Guenther, Isenberg, Ivey, Knopf, Lu, Luo and Ni7]), we get
and
By eliminating f from (1.5) and (1.6), we get that
![]() $a(t)$
satisfies
$a(t)$
satisfies
 $$ \begin{align} a(t)^2a_t(t)a_{ttt}(t)=&a(t)a_t(t)^2a_{tt}(t)+a(t)^2a_{tt}(t)^2-(n-1)a(t)a_{tt}(t)\notag\\ &\qquad -\lambda a(t)^3a_{tt}(t)-(n-1)a_t(t)^2+(n-1)a_t(t)^4. \end{align} $$
$$ \begin{align} a(t)^2a_t(t)a_{ttt}(t)=&a(t)a_t(t)^2a_{tt}(t)+a(t)^2a_{tt}(t)^2-(n-1)a(t)a_{tt}(t)\notag\\ &\qquad -\lambda a(t)^3a_{tt}(t)-(n-1)a_t(t)^2+(n-1)a_t(t)^4. \end{align} $$
Note that we can express g as
 $$ \begin{align} g=\frac{da^2}{h(a^2)}+a^2\,g_{S^n}, \end{align} $$
$$ \begin{align} g=\frac{da^2}{h(a^2)}+a^2\,g_{S^n}, \end{align} $$
where
![]() $h(r)$
,
$h(r)$
,
![]() $r=a^2\ge 0$
, and
$r=a^2\ge 0$
, and
![]() $a=a(t)$
satisfies
$a=a(t)$
satisfies
Then, by (1.7) and a direct computation, h satisfies
We are now interested in rotational symmetric gradient Ricci soliton which blows up at
![]() $r=0$
at the rate
$r=0$
at the rate
for some constants
![]() $\alpha>0$
and
$\alpha>0$
and
![]() $c_0>0$
. Let
$c_0>0$
. Let
By (1.10), (1.12), and a direct computation, w satisfies
 $$ \begin{align} 2r^2w(r)w_{rr}(r)=\ &2\alpha r w(r)w_r(r)+(n-1)(\alpha -1)r^{\alpha}w(r)+\alpha\lambda r^{\alpha +1}w(r)\notag\\ &\quad -(n-1)r^{\alpha +1}w_r(r)-\lambda r^{\alpha +2}w_r(r)+r^2w_r(r)^2\notag\\ &\quad -(\alpha^2+2\alpha -(n-1))w(r)^2. \end{align} $$
$$ \begin{align} 2r^2w(r)w_{rr}(r)=\ &2\alpha r w(r)w_r(r)+(n-1)(\alpha -1)r^{\alpha}w(r)+\alpha\lambda r^{\alpha +1}w(r)\notag\\ &\quad -(n-1)r^{\alpha +1}w_r(r)-\lambda r^{\alpha +2}w_r(r)+r^2w_r(r)^2\notag\\ &\quad -(\alpha^2+2\alpha -(n-1))w(r)^2. \end{align} $$
Unless stated otherwise, we now let
![]() $\alpha =\sqrt {n}-1>0$
for the rest of the paper. Then
$\alpha =\sqrt {n}-1>0$
for the rest of the paper. Then
![]() $\alpha ^2+2\alpha -(n-1)=0$
. Hence, by (1.13), w satisfies
$\alpha ^2+2\alpha -(n-1)=0$
. Hence, by (1.13), w satisfies
 $$ \begin{align} 2r^2w(r)w_{rr}(r)=\ &2\alpha r w(r)w_r(r)+(n-1)(\alpha -1)r^{\alpha}w(r)+\alpha\lambda r^{\alpha +1}w(r)\notag\\ &\quad -(n-1)r^{\alpha +1}w_r(r)-\lambda r^{\alpha +2}w_r(r)+r^2w_r(r)^2 \end{align} $$
$$ \begin{align} 2r^2w(r)w_{rr}(r)=\ &2\alpha r w(r)w_r(r)+(n-1)(\alpha -1)r^{\alpha}w(r)+\alpha\lambda r^{\alpha +1}w(r)\notag\\ &\quad -(n-1)r^{\alpha +1}w_r(r)-\lambda r^{\alpha +2}w_r(r)+r^2w_r(r)^2 \end{align} $$
with
![]() $\alpha =\sqrt {n}-1>0$
. We also impose the condition
$\alpha =\sqrt {n}-1>0$
. We also impose the condition
 $$ \begin{align} t=\int_0^{a(t)}\frac{d\rho}{\sqrt{h(\rho^2)}}. \end{align} $$
$$ \begin{align} t=\int_0^{a(t)}\frac{d\rho}{\sqrt{h(\rho^2)}}. \end{align} $$
In the paper [Reference Bryant4], Bryant by using power series expansion around the singular point at the origin gave the local existence of singular solution of (1.10) near the origin which blows up at the rate (1.11) for the case
![]() $n=2$
. On the other hand, by using phase plane analysis of the functions
$n=2$
. On the other hand, by using phase plane analysis of the functions
 $$ \begin{align*} W=\frac{1}{f_t(t)+n\frac{a_t(t)}{a(t)}},\quad X=\sqrt{n}W\frac{a_t(t)}{a(t)},\quad Y=\frac{\sqrt(n-1)W}{a(t)}, \end{align*} $$
$$ \begin{align*} W=\frac{1}{f_t(t)+n\frac{a_t(t)}{a(t)}},\quad X=\sqrt{n}W\frac{a_t(t)}{a(t)},\quad Y=\frac{\sqrt(n-1)W}{a(t)}, \end{align*} $$
Alexakis, Chen, and Fournodavlos [Reference Alexakis, Chen and Fournodavlos1] gave a sketch of proof for the local existence of singular solution
![]() $(a(t), f(t))$
, of (1.5) and (1.6), near the origin and its asymptotic behavior as
$(a(t), f(t))$
, of (1.5) and (1.6), near the origin and its asymptotic behavior as
![]() $t\to 0^+$
for the case
$t\to 0^+$
for the case
![]() $n\ge 2$
. When
$n\ge 2$
. When
![]() $\lambda =0$
, the existence of global solution
$\lambda =0$
, the existence of global solution
![]() $(a(t), f(t))$
, of (1.5) and (1.6), in
$(a(t), f(t))$
, of (1.5) and (1.6), in
![]() $(0,\infty )$
is also mentioned without detailed proof in [Reference Alexakis, Chen and Fournodavlos1].
$(0,\infty )$
is also mentioned without detailed proof in [Reference Alexakis, Chen and Fournodavlos1].
In this paper, we will use fixed-point argument for the function w given by (1.12) to give a new proof of the local existence of solution h of (1.10) satisfying (1.11) for any constants
![]() $\lambda \in {\mathbb {R}}$
,
$\lambda \in {\mathbb {R}}$
,
![]() $c_0>0$
, and
$c_0>0$
, and
![]() $2\le n\in {\mathbb Z}^+$
. For
$2\le n\in {\mathbb Z}^+$
. For
![]() $\lambda \ge 0$
, we will then use a continuation method to extend the local singular solutions of (1.10) and (1.11) to global solutions of (1.10) and (1.11). We will also prove the higher-order asymptotic behavior of the local solutions of (1.10) and (1.11), near the origin.
$\lambda \ge 0$
, we will then use a continuation method to extend the local singular solutions of (1.10) and (1.11) to global solutions of (1.10) and (1.11). We will also prove the higher-order asymptotic behavior of the local solutions of (1.10) and (1.11), near the origin.
The main results we obtain in this paper are the following.
Theorem 1.1 Let
![]() $2\le n\in {\mathbb Z}^+$
,
$2\le n\in {\mathbb Z}^+$
,
![]() $\lambda \ge 0$
,
$\lambda \ge 0$
,
![]() $\alpha =\sqrt {n}-1$
,
$\alpha =\sqrt {n}-1$
,
![]() $c_0>0$
,
$c_0>0$
,
![]() $c_1\in {\mathbb {R}}$
, and
$c_1\in {\mathbb {R}}$
, and
There exists a unique solution
![]() $h\in C^2((0,\infty ))$
of (1.10) in
$h\in C^2((0,\infty ))$
of (1.10) in
![]() $(0,\infty )$
which satisfies (1.11) and (2.4) in
$(0,\infty )$
which satisfies (1.11) and (2.4) in
![]() $(0,\varepsilon )$
with w given by (1.12) for some constant
$(0,\varepsilon )$
with w given by (1.12) for some constant
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Theorem 1.2 Let
![]() $4<n\in {\mathbb Z}^+$
,
$4<n\in {\mathbb Z}^+$
,
![]() $\lambda \ge 0$
,
$\lambda \ge 0$
,
![]() $\alpha =\sqrt {n}-1$
,
$\alpha =\sqrt {n}-1$
,
![]() $c_0>0$
,
$c_0>0$
,
![]() $c_1\in {\mathbb {R}}$
, and
$c_1\in {\mathbb {R}}$
, and
![]() $c_2$
be given by (1.17). Then there exists a constant
$c_2$
be given by (1.17). Then there exists a constant
![]() $0<\delta _0<1$
such that (1.10) has a unique solution
$0<\delta _0<1$
such that (1.10) has a unique solution
![]() ${h\in C^2((0,\infty ))}$
in
${h\in C^2((0,\infty ))}$
in
![]() $(0,\infty )$
which satisfies (1.11) and
$(0,\infty )$
which satisfies (1.11) and
 $$ \begin{align} h(r)=&\frac{1}{r^{\alpha}}\left\{c_0-\frac{c_2}{\alpha}r^{\alpha}+\left(\frac{c_1}{\alpha+1}-\frac{\alpha\lambda}{2(\alpha +1)^2}\right)r^{\alpha +1}+\frac{\alpha\lambda}{2\alpha +2}r^{\alpha +1}\log r \right.\notag\\ &\quad \left.+\frac{c_2^2+(n-1)c_2}{4c_0\alpha (\alpha -1)}r^{2\alpha}+o(1)r^{2\alpha}\right\}\quad\forall 0<r\le \delta_0. \end{align} $$
$$ \begin{align} h(r)=&\frac{1}{r^{\alpha}}\left\{c_0-\frac{c_2}{\alpha}r^{\alpha}+\left(\frac{c_1}{\alpha+1}-\frac{\alpha\lambda}{2(\alpha +1)^2}\right)r^{\alpha +1}+\frac{\alpha\lambda}{2\alpha +2}r^{\alpha +1}\log r \right.\notag\\ &\quad \left.+\frac{c_2^2+(n-1)c_2}{4c_0\alpha (\alpha -1)}r^{2\alpha}+o(1)r^{2\alpha}\right\}\quad\forall 0<r\le \delta_0. \end{align} $$
Moreover,
 $$ \begin{align} h_r(r)=&\frac{1}{r^{\alpha+1}}\left\{-\alpha c_0+\left(\frac{c_1}{\alpha+1}+\frac{\alpha^2\lambda}{2(\alpha +1)^2}\right)r^{\alpha +1}+\frac{\alpha\lambda}{2\alpha +2}r^{\alpha +1}\log r \right.\notag\\ &\quad \left.+\frac{c_2^2+(n-1)c_2}{4c_0(\alpha -1)}r^{2\alpha}+o(1)r^{2\alpha}\right\}\quad\forall 0<r\le \delta_0. \end{align} $$
$$ \begin{align} h_r(r)=&\frac{1}{r^{\alpha+1}}\left\{-\alpha c_0+\left(\frac{c_1}{\alpha+1}+\frac{\alpha^2\lambda}{2(\alpha +1)^2}\right)r^{\alpha +1}+\frac{\alpha\lambda}{2\alpha +2}r^{\alpha +1}\log r \right.\notag\\ &\quad \left.+\frac{c_2^2+(n-1)c_2}{4c_0(\alpha -1)}r^{2\alpha}+o(1)r^{2\alpha}\right\}\quad\forall 0<r\le \delta_0. \end{align} $$
Theorem 1.3 Let
![]() $n\in \{2,3,4\}$
,
$n\in \{2,3,4\}$
,
![]() $\alpha =\sqrt {n}-1$
,
$\alpha =\sqrt {n}-1$
,
![]() $\lambda \ge 0$
,
$\lambda \ge 0$
,
![]() $c_0>0$
,
$c_0>0$
,
![]() $c_1\in {\mathbb {R}}$
, and
$c_1\in {\mathbb {R}}$
, and
![]() $c_2$
be given by (1.17). Let
$c_2$
be given by (1.17). Let
![]() $h\in C^2((0,\infty ))$
be given by Theorem 1.1. Then there exists a constant
$h\in C^2((0,\infty ))$
be given by Theorem 1.1. Then there exists a constant
![]() ${0<\delta _0<1}$
such that
${0<\delta _0<1}$
such that
 $$ \begin{align} h(r)=\left\{\begin{aligned} &\frac{1}{r^{\alpha}}\left(c_0-\frac{c_2}{\alpha}r^{\alpha}-\frac{c_2(c_2+n-1)}{4c_0\alpha (1-\alpha)}r^{2\alpha}+o(1)r^{2\alpha}\right), \quad\forall 0<r\le \delta_0\,\mbox{ if }n=2,3,\\ &\frac{1}{r}\left(c_0+\frac{\lambda}{4}r^2\log r+o(1)r^2|\log r|\right), \qquad\qquad\quad\forall 0<r\le \delta_0\quad\mbox{ if }n=4. \end{aligned} \right. \end{align} $$
$$ \begin{align} h(r)=\left\{\begin{aligned} &\frac{1}{r^{\alpha}}\left(c_0-\frac{c_2}{\alpha}r^{\alpha}-\frac{c_2(c_2+n-1)}{4c_0\alpha (1-\alpha)}r^{2\alpha}+o(1)r^{2\alpha}\right), \quad\forall 0<r\le \delta_0\,\mbox{ if }n=2,3,\\ &\frac{1}{r}\left(c_0+\frac{\lambda}{4}r^2\log r+o(1)r^2|\log r|\right), \qquad\qquad\quad\forall 0<r\le \delta_0\quad\mbox{ if }n=4. \end{aligned} \right. \end{align} $$
Moreover,
 $$ \begin{align} h_r(r)=\left\{\begin{aligned} &\frac{1}{r^{\alpha+1}}\left(-\alpha c_0-\frac{c_2(c_2+n-1)}{4c_0(1-\alpha)}r^{2\alpha}+o(1)r^{2\alpha}\right),\quad\forall 0<r\le \delta_0\,\mbox{ if }n=2,3,\\ &\frac{1}{r^2}\left(-c_0+\frac{\lambda}{4}r^2\log r+o(1)r^2|\log r|\right),\qquad\quad\forall 0<r\le \delta_0\quad\mbox{ if }n=4. \end{aligned} \right. \end{align} $$
$$ \begin{align} h_r(r)=\left\{\begin{aligned} &\frac{1}{r^{\alpha+1}}\left(-\alpha c_0-\frac{c_2(c_2+n-1)}{4c_0(1-\alpha)}r^{2\alpha}+o(1)r^{2\alpha}\right),\quad\forall 0<r\le \delta_0\,\mbox{ if }n=2,3,\\ &\frac{1}{r^2}\left(-c_0+\frac{\lambda}{4}r^2\log r+o(1)r^2|\log r|\right),\qquad\quad\forall 0<r\le \delta_0\quad\mbox{ if }n=4. \end{aligned} \right. \end{align} $$
Note that the singular solutions h of (1.10) in
![]() $(0,\infty )$
given by Theorems 1.1–1.3 satisfy (1.11) with
$(0,\infty )$
given by Theorems 1.1–1.3 satisfy (1.11) with
![]() $\alpha =\sqrt {n}-1$
. Moreover, by (1.2), the solitons constructed in Theorems 1.1 and 1.2 are complete at
$\alpha =\sqrt {n}-1$
. Moreover, by (1.2), the solitons constructed in Theorems 1.1 and 1.2 are complete at
![]() $t=+\infty $
. A natural question to ask is that does there exist any other singular solution of (1.10) in
$t=+\infty $
. A natural question to ask is that does there exist any other singular solution of (1.10) in
![]() $(0,\varepsilon )$
for some constant
$(0,\varepsilon )$
for some constant
![]() $\varepsilon>0$
which blow-up at a different rate at the origin. We answer this question in the negative. More precisely, we prove the following result.
$\varepsilon>0$
which blow-up at a different rate at the origin. We answer this question in the negative. More precisely, we prove the following result.
Theorem 1.4 Let
![]() $2\le n\in {\mathbb Z}^+$
,
$2\le n\in {\mathbb Z}^+$
,
![]() $\lambda \in {\mathbb {R}}$
,
$\lambda \in {\mathbb {R}}$
,
![]() $\varepsilon>0$
, and
$\varepsilon>0$
, and
![]() $c_0>0$
. Suppose
$c_0>0$
. Suppose
![]() $h\in C^2((0,\varepsilon ))$
is a solution of (1.10) in
$h\in C^2((0,\varepsilon ))$
is a solution of (1.10) in
![]() $(0,\varepsilon )$
which satisfies (1.11) for some constant
$(0,\varepsilon )$
which satisfies (1.11) for some constant
![]() $\alpha>0$
. Then
$\alpha>0$
. Then
![]() $\alpha =\sqrt {n}-1$
.
$\alpha =\sqrt {n}-1$
.
The plan of the paper is as follows. In Section 2, we will prove the local existence of infinitely many singular solutions of (1.10) and (1.11), in a neighborhood of the origin, and conditions for uniqueness of local singular solutions are given. We will also prove the higher-order asymptotic behavior of these local solutions near the origin. In Section 3, we will prove the global existence of infinitely many singular solutions of (1.10) and (1.11) and conditions for uniqueness of global singular solution are given. In Section 4, we will prove the asymptotic behavior of
![]() $a(t)$
near the origin.
$a(t)$
near the origin.
2 Local existence, uniqueness, and asymptotic behavior of singular solutions near the origin
In this section, for any
![]() $2\le n\in {\mathbb Z}^+$
,
$2\le n\in {\mathbb Z}^+$
,
![]() $\lambda \in {\mathbb {R}}$
, and
$\lambda \in {\mathbb {R}}$
, and
![]() $c_0>0$
, we will prove the local existence of infinitely many singular solutions of (1.10) in
$c_0>0$
, we will prove the local existence of infinitely many singular solutions of (1.10) in
![]() $(0,\varepsilon )$
which satisfy (1.11) for some constant
$(0,\varepsilon )$
which satisfy (1.11) for some constant
![]() $\varepsilon>0$
. Under some mild conditions on the singular solutions of (1.10) in
$\varepsilon>0$
. Under some mild conditions on the singular solutions of (1.10) in
![]() $(0,\varepsilon )$
, we will also prove the uniqueness of local singular solutions of (1.10) in
$(0,\varepsilon )$
, we will also prove the uniqueness of local singular solutions of (1.10) in
![]() $(0,\varepsilon )$
satisfying (1.11). We first observe that if
$(0,\varepsilon )$
satisfying (1.11). We first observe that if
![]() $h\in C^2((0,\varepsilon ];{\mathbb {R}}^+)$
is a solution of (1.10) in
$h\in C^2((0,\varepsilon ];{\mathbb {R}}^+)$
is a solution of (1.10) in
![]() $(0,\varepsilon ]$
for some constant
$(0,\varepsilon ]$
for some constant
![]() $\varepsilon>0$
which satisfies (1.11) for some constant
$\varepsilon>0$
which satisfies (1.11) for some constant
![]() $c_0>0$
and w is given by (1.12) with
$c_0>0$
and w is given by (1.12) with
![]() $\alpha =\sqrt {n}-1$
, then by (1.11), (1.12), and (1.14),
$\alpha =\sqrt {n}-1$
, then by (1.11), (1.12), and (1.14),
![]() $w>0$
satisfies
$w>0$
satisfies
 $$ \begin{align} w_{rr}(r)=&\frac{\alpha}{r}w_r(r)+\frac{(n-1)(\alpha -1)}{2}r^{\alpha-2}+\frac{\alpha\lambda}{2} r^{\alpha-1}-\frac{(n-1)r^{\alpha-1}w_r(r)}{2w(r)} \notag\\ &\qquad -\frac{\lambda r^{\alpha}w_r(r)}{2w(r)}+\frac{w_r(r)^2}{2w(r)} \end{align} $$
$$ \begin{align} w_{rr}(r)=&\frac{\alpha}{r}w_r(r)+\frac{(n-1)(\alpha -1)}{2}r^{\alpha-2}+\frac{\alpha\lambda}{2} r^{\alpha-1}-\frac{(n-1)r^{\alpha-1}w_r(r)}{2w(r)} \notag\\ &\qquad -\frac{\lambda r^{\alpha}w_r(r)}{2w(r)}+\frac{w_r(r)^2}{2w(r)} \end{align} $$
in
![]() $(0,\varepsilon ]$
and
$(0,\varepsilon ]$
and
if
![]() $w\in C([0,\varepsilon ];{\mathbb {R}}^+)$
. Hence, the existence of solution
$w\in C([0,\varepsilon ];{\mathbb {R}}^+)$
. Hence, the existence of solution
![]() $h\in C^2((0,\varepsilon ];{\mathbb {R}}^+)$
of (1.10) in
$h\in C^2((0,\varepsilon ];{\mathbb {R}}^+)$
of (1.10) in
![]() $(0,\varepsilon ]$
which satisfies (1.11) is equivalent to the existence of solution
$(0,\varepsilon ]$
which satisfies (1.11) is equivalent to the existence of solution
![]() $w\in C^2((0,\varepsilon ];{\mathbb {R}}^+)\cap C([0,\varepsilon ];{\mathbb {R}}^+)$
of (2.1) in
$w\in C^2((0,\varepsilon ];{\mathbb {R}}^+)\cap C([0,\varepsilon ];{\mathbb {R}}^+)$
of (2.1) in
![]() $(0,\varepsilon ]$
which satisfies (2.2). Note that (2.1) is equivalent to
$(0,\varepsilon ]$
which satisfies (2.2). Note that (2.1) is equivalent to
 $$ \begin{align} (r^{-\alpha}w_r)_r(r)=&c_2r^{-2}+\frac{\alpha\lambda}{2}r^{-1} -\frac{(n-1)r^{-1} w_r(r)}{2w(r)}-\frac{\lambda w_r(r)}{2w(r)}+\frac{r^{-\alpha}w_r(r)^2}{2w(r)} \end{align} $$
$$ \begin{align} (r^{-\alpha}w_r)_r(r)=&c_2r^{-2}+\frac{\alpha\lambda}{2}r^{-1} -\frac{(n-1)r^{-1} w_r(r)}{2w(r)}-\frac{\lambda w_r(r)}{2w(r)}+\frac{r^{-\alpha}w_r(r)^2}{2w(r)} \end{align} $$
 $$ \begin{align} \Leftrightarrow\quad r^{-\alpha}w_r(r)=&-c_2r^{-1}+c_1+\frac{\alpha\lambda}{2}\log r +\frac{(n-1)}{2}\int_r^{\varepsilon}\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho\notag\\ &\quad -\frac{\lambda}{2}\int_0^r\frac{w_r(\rho)}{w(\rho)}\,d\rho-\frac{1}{2} \int_r^{\varepsilon}\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho\quad\forall 0<r\le\varepsilon\notag\\ \Leftrightarrow\qquad\,\, w_r(r)=&-c_2r^{\alpha-1}+c_1r^{\alpha}+\frac{\alpha\lambda}{2}r^{\alpha}\log r +r^{\alpha}\left\{\frac{(n-1)}{2}\int_r^{\varepsilon}\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho \right.\notag\\ &\quad \left.-\frac{\lambda}{2}\int_0^r\frac{w_r(\rho)}{w(\rho)}\,d\rho-\frac{1}{2} \int_r^{\varepsilon}\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho\right\}\quad\forall 0<r\le\varepsilon \end{align} $$
$$ \begin{align} \Leftrightarrow\quad r^{-\alpha}w_r(r)=&-c_2r^{-1}+c_1+\frac{\alpha\lambda}{2}\log r +\frac{(n-1)}{2}\int_r^{\varepsilon}\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho\notag\\ &\quad -\frac{\lambda}{2}\int_0^r\frac{w_r(\rho)}{w(\rho)}\,d\rho-\frac{1}{2} \int_r^{\varepsilon}\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho\quad\forall 0<r\le\varepsilon\notag\\ \Leftrightarrow\qquad\,\, w_r(r)=&-c_2r^{\alpha-1}+c_1r^{\alpha}+\frac{\alpha\lambda}{2}r^{\alpha}\log r +r^{\alpha}\left\{\frac{(n-1)}{2}\int_r^{\varepsilon}\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho \right.\notag\\ &\quad \left.-\frac{\lambda}{2}\int_0^r\frac{w_r(\rho)}{w(\rho)}\,d\rho-\frac{1}{2} \int_r^{\varepsilon}\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho\right\}\quad\forall 0<r\le\varepsilon \end{align} $$
for some constant
![]() $c_1\in {\mathbb {R}}$
. This suggests one to use fixed-point argument to prove the existence of solution
$c_1\in {\mathbb {R}}$
. This suggests one to use fixed-point argument to prove the existence of solution
![]() $w\in C^2((0,\varepsilon ];{\mathbb {R}}^+)\cap C([0,\varepsilon ];{\mathbb {R}}^+)$
of (2.1) in
$w\in C^2((0,\varepsilon ];{\mathbb {R}}^+)\cap C([0,\varepsilon ];{\mathbb {R}}^+)$
of (2.1) in
![]() $(0,\varepsilon ]$
which satisfies (2.2).
$(0,\varepsilon ]$
which satisfies (2.2).
Proposition Let
![]() $2\le n\in {\mathbb Z}^+$
,
$2\le n\in {\mathbb Z}^+$
,
![]() $\alpha =\sqrt {n}-1$
,
$\alpha =\sqrt {n}-1$
,
![]() $\lambda , c_1\in {\mathbb {R}}$
,
$\lambda , c_1\in {\mathbb {R}}$
,
![]() $c_0>0$
, and let
$c_0>0$
, and let
![]() $c_2$
be given by (1.17). Then there exists a constant
$c_2$
be given by (1.17). Then there exists a constant
![]() $0<\varepsilon <1$
such that (2.1) has a unique solution
$0<\varepsilon <1$
such that (2.1) has a unique solution
![]() $w\in C^2((0,\varepsilon ];{\mathbb {R}}^+)\cap C([0,\varepsilon ];{\mathbb {R}}^+)$
in
$w\in C^2((0,\varepsilon ];{\mathbb {R}}^+)\cap C([0,\varepsilon ];{\mathbb {R}}^+)$
in
![]() $(0,\varepsilon ]$
which satisfies (2.2) and (2.4). Moreover,
$(0,\varepsilon ]$
which satisfies (2.2) and (2.4). Moreover,
holds.
Proof For any
![]() $\varepsilon>0$
, we define the Banach space
$\varepsilon>0$
, we define the Banach space
 $$ \begin{align*} {\mathcal X}_\varepsilon:=&\{(w,v): w\in C( [0,\varepsilon];{\mathbb{R}}^+),v\in C( (0,\varepsilon];{\mathbb{R}})\mbox{ such that }r^{1-\alpha}v(r)\mbox{ can be }\\ &\mbox{ extended to a function in }C( [0,\varepsilon];{\mathbb{R}})\} \end{align*} $$
$$ \begin{align*} {\mathcal X}_\varepsilon:=&\{(w,v): w\in C( [0,\varepsilon];{\mathbb{R}}^+),v\in C( (0,\varepsilon];{\mathbb{R}})\mbox{ such that }r^{1-\alpha}v(r)\mbox{ can be }\\ &\mbox{ extended to a function in }C( [0,\varepsilon];{\mathbb{R}})\} \end{align*} $$
with a norm given by
For any
![]() $(w,v)\in {\mathcal X}_\varepsilon ,$
we define
$(w,v)\in {\mathcal X}_\varepsilon ,$
we define
where
 $$ \begin{align} \left\{\begin{aligned} \Phi_1(w,v)(r)=\ &c_0+\int_0^r v(\rho)\,d\rho,\\ \Phi_2(w,v)(r)=&-c_2r^{\alpha-1}+c_1r^{\alpha}+\frac{\alpha\lambda}{2}r^{\alpha}\log r +r^{\alpha}\left\{\frac{(n-1)}{2}\int_r^{\varepsilon}\frac{\rho^{-1}v(\rho)}{w(\rho)}\,d\rho \right.\\ &\quad \left.-\frac{\lambda}{2}\int_0^r\frac{v(\rho)}{w(\rho)}\,d\rho-\frac{1}{2} \int_r^{\varepsilon}\frac{\rho^{-\alpha}v(\rho)^2}{w(\rho)}\,d\rho\right\} \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{\begin{aligned} \Phi_1(w,v)(r)=\ &c_0+\int_0^r v(\rho)\,d\rho,\\ \Phi_2(w,v)(r)=&-c_2r^{\alpha-1}+c_1r^{\alpha}+\frac{\alpha\lambda}{2}r^{\alpha}\log r +r^{\alpha}\left\{\frac{(n-1)}{2}\int_r^{\varepsilon}\frac{\rho^{-1}v(\rho)}{w(\rho)}\,d\rho \right.\\ &\quad \left.-\frac{\lambda}{2}\int_0^r\frac{v(\rho)}{w(\rho)}\,d\rho-\frac{1}{2} \int_r^{\varepsilon}\frac{\rho^{-\alpha}v(\rho)^2}{w(\rho)}\,d\rho\right\} \end{aligned} \right. \end{align} $$
for any
![]() $0<r\leq \varepsilon $
. Let
$0<r\leq \varepsilon $
. Let
Since
![]() $(c_0,-c_2r^{\alpha -1})\in {\mathcal D}_{\varepsilon }$
,
$(c_0,-c_2r^{\alpha -1})\in {\mathcal D}_{\varepsilon }$
,
![]() ${\mathcal D}_{\varepsilon }\ne \phi $
. We will show that there exists
${\mathcal D}_{\varepsilon }\ne \phi $
. We will show that there exists
![]() $\varepsilon \in (0,1/2)$
such that the map
$\varepsilon \in (0,1/2)$
such that the map
![]() $(w,v)\mapsto \Phi (w,v)$
has a unique fixed point in the closed subspace
$(w,v)\mapsto \Phi (w,v)$
has a unique fixed point in the closed subspace
![]() ${\mathcal D}_{\varepsilon }$
. Let
${\mathcal D}_{\varepsilon }$
. Let
 $$ \begin{align*} \varepsilon_1=\min\left(\frac{1}{2}, \left(\frac{c_0\alpha}{10|c_2|+c_0}\right)^{1/\alpha}\right). \end{align*} $$
$$ \begin{align*} \varepsilon_1=\min\left(\frac{1}{2}, \left(\frac{c_0\alpha}{10|c_2|+c_0}\right)^{1/\alpha}\right). \end{align*} $$
We first prove that
![]() $\Phi ({\mathcal D}_{\varepsilon })\subset {\mathcal D}_{\varepsilon }$
for sufficiently small
$\Phi ({\mathcal D}_{\varepsilon })\subset {\mathcal D}_{\varepsilon }$
for sufficiently small
![]() $\varepsilon \in (0,\varepsilon _1)$
. For any
$\varepsilon \in (0,\varepsilon _1)$
. For any
![]() $\varepsilon \in (0,\varepsilon _1)$
,
$\varepsilon \in (0,\varepsilon _1)$
,
![]() $(w,v)\in {\mathcal D}_{\varepsilon }$
,
$(w,v)\in {\mathcal D}_{\varepsilon }$
,
![]() $0\leq r<\varepsilon $
, by (2.7), we have
$0\leq r<\varepsilon $
, by (2.7), we have
and
where
![]() $c_3=|c_2|+(c_0/10)$
. Hence, by (2.9),
$c_3=|c_2|+(c_0/10)$
. Hence, by (2.9),
 $$ \begin{align} &|\Phi_1(w,v)(r)-c_0|\le\int_0^rc_3\rho^{\alpha -1}\,d\rho=(c_3/\alpha)r^{\alpha}\le (c_3/\alpha)\varepsilon^{\alpha}\le c_0/10\quad\forall 0<r\le\varepsilon\notag\\ \Rightarrow\quad&\|\Phi_1(w,v)-c_0\|_{L^{\infty}\left([0, \varepsilon]\right)}\le c_0/10\quad\mbox{ and }\quad \|\Phi_1(w,v)\|_{L^{\infty}\left([0, \varepsilon]\right)}\le 11c_0/10. \end{align} $$
$$ \begin{align} &|\Phi_1(w,v)(r)-c_0|\le\int_0^rc_3\rho^{\alpha -1}\,d\rho=(c_3/\alpha)r^{\alpha}\le (c_3/\alpha)\varepsilon^{\alpha}\le c_0/10\quad\forall 0<r\le\varepsilon\notag\\ \Rightarrow\quad&\|\Phi_1(w,v)-c_0\|_{L^{\infty}\left([0, \varepsilon]\right)}\le c_0/10\quad\mbox{ and }\quad \|\Phi_1(w,v)\|_{L^{\infty}\left([0, \varepsilon]\right)}\le 11c_0/10. \end{align} $$
We now choose
![]() $c_4>1$
such that
$c_4>1$
such that
Then, by (2.8), (2.9), and (2.11), for any
![]() $0<r\le \varepsilon $
,
$0<r\le \varepsilon $
,
 $$ \begin{align} r\left|\int_r^{\varepsilon}\frac{\rho^{-1}v(\rho)}{w(\rho)}\,d\rho\right| \le&\frac{10c_3r}{9c_0}\int_r^{\varepsilon}\rho^{\alpha-2}\,d\rho \le\left\{\begin{aligned} &\frac{10c_3r(r^{\alpha-1}+\varepsilon^{\alpha-1})}{9c_0|\alpha-1|},\qquad\ \mbox{ if }n \ne 4\\ &\frac{10c_3r(|\log r|+|\log \varepsilon|)}{9c_0},\quad\mbox{if }n=4 \end{aligned} \right.\notag\\\le&\left\{\begin{aligned} &\frac{20c_3\varepsilon^{\alpha}}{9c_0|\alpha -1|},\quad\,\mbox{ if }n \ne 4,\\ &\frac{20c_3c_4\varepsilon^{1/2}}{9c_0},\quad\mbox{ if }n=4, \end{aligned} \right. \end{align} $$
$$ \begin{align} r\left|\int_r^{\varepsilon}\frac{\rho^{-1}v(\rho)}{w(\rho)}\,d\rho\right| \le&\frac{10c_3r}{9c_0}\int_r^{\varepsilon}\rho^{\alpha-2}\,d\rho \le\left\{\begin{aligned} &\frac{10c_3r(r^{\alpha-1}+\varepsilon^{\alpha-1})}{9c_0|\alpha-1|},\qquad\ \mbox{ if }n \ne 4\\ &\frac{10c_3r(|\log r|+|\log \varepsilon|)}{9c_0},\quad\mbox{if }n=4 \end{aligned} \right.\notag\\\le&\left\{\begin{aligned} &\frac{20c_3\varepsilon^{\alpha}}{9c_0|\alpha -1|},\quad\,\mbox{ if }n \ne 4,\\ &\frac{20c_3c_4\varepsilon^{1/2}}{9c_0},\quad\mbox{ if }n=4, \end{aligned} \right. \end{align} $$
 $$ \begin{align} r\left|\int_0^r\frac{v(\rho)}{w(\rho)}\,d\rho\right| \le\frac{10c_3r}{9c_0}\int_0^r\rho^{\alpha-1}\,d\rho =\frac{10c_3r^{\alpha+1}}{9c_0\alpha}\le\frac{10c_3\varepsilon^{\alpha+1}}{9c_0\alpha} \end{align} $$
$$ \begin{align} r\left|\int_0^r\frac{v(\rho)}{w(\rho)}\,d\rho\right| \le\frac{10c_3r}{9c_0}\int_0^r\rho^{\alpha-1}\,d\rho =\frac{10c_3r^{\alpha+1}}{9c_0\alpha}\le\frac{10c_3\varepsilon^{\alpha+1}}{9c_0\alpha} \end{align} $$
and
 $$ \begin{align} r\left|\int_r^{\varepsilon}\frac{\rho^{-\alpha}v(\rho)^2}{w(\rho)}\,d\rho\right| \le&\frac{10c_3^2r}{9c_0}\int_r^{\varepsilon}\rho^{\alpha-2}\,d\rho \le\left\{\begin{aligned} &\frac{10c_3^2r(r^{\alpha-1}+\varepsilon^{\alpha-1})}{9c_0|\alpha-1|},\qquad\ \ \ \mbox{if }n \ne 4,\\ &\frac{20c_3^2r(|\log r|+|\log \varepsilon|)}{9c_0},\quad\mbox{if }n=4, \end{aligned} \right.\notag\\\le&\left\{\begin{aligned} &\frac{20c_3^2\varepsilon^{\alpha}}{9c_0|\alpha -1|},\quad\mbox{ if }n \ne 4,\\ &\frac{20c_3^2c_4\varepsilon^{1/2}}{9c_0},\quad\mbox{ if }n=4. \end{aligned} \right. \end{align} $$
$$ \begin{align} r\left|\int_r^{\varepsilon}\frac{\rho^{-\alpha}v(\rho)^2}{w(\rho)}\,d\rho\right| \le&\frac{10c_3^2r}{9c_0}\int_r^{\varepsilon}\rho^{\alpha-2}\,d\rho \le\left\{\begin{aligned} &\frac{10c_3^2r(r^{\alpha-1}+\varepsilon^{\alpha-1})}{9c_0|\alpha-1|},\qquad\ \ \ \mbox{if }n \ne 4,\\ &\frac{20c_3^2r(|\log r|+|\log \varepsilon|)}{9c_0},\quad\mbox{if }n=4, \end{aligned} \right.\notag\\\le&\left\{\begin{aligned} &\frac{20c_3^2\varepsilon^{\alpha}}{9c_0|\alpha -1|},\quad\mbox{ if }n \ne 4,\\ &\frac{20c_3^2c_4\varepsilon^{1/2}}{9c_0},\quad\mbox{ if }n=4. \end{aligned} \right. \end{align} $$
Let
 $$ \begin{align*} c_5=\left\{\begin{aligned} &\frac{4n(c_3+c_3^2)}{c_0|\alpha-1|}+\frac{c_3|\lambda|}{c_0\alpha},\qquad\mbox{ if }n \ne 4,\\ &\frac{4nc_4(c_3+c_3^2)}{c_0}+\frac{c_3|\lambda|}{c_0\alpha}, \,\quad\mbox{ if }n=4. \end{aligned} \right. \end{align*} $$
$$ \begin{align*} c_5=\left\{\begin{aligned} &\frac{4n(c_3+c_3^2)}{c_0|\alpha-1|}+\frac{c_3|\lambda|}{c_0\alpha},\qquad\mbox{ if }n \ne 4,\\ &\frac{4nc_4(c_3+c_3^2)}{c_0}+\frac{c_3|\lambda|}{c_0\alpha}, \,\quad\mbox{ if }n=4. \end{aligned} \right. \end{align*} $$
 $$ \begin{align} &r^{1-\alpha}\left|\Phi_2(w,v)(r)+c_2r^{\alpha-1}\right|\notag\\ \le&|c_1|r+\frac{\alpha |\lambda|}{2}r|\log r| +\frac{(n-1)r}{2}\left|\int_r^{\varepsilon}\frac{\rho^{-1}v(\rho)}{w(\rho)}\,d\rho\right|+\frac{|\lambda|r}{2}\left|\int_0^r\frac{v(\rho)}{w(\rho)}\,d\rho\right|+\frac{r}{2} \left|\int_r^{\varepsilon}\frac{\rho^{-\alpha}v(\rho)^2}{w(\rho)}\,d\rho\right| \notag\\ \le&|c_1|\varepsilon+\frac{\alpha |\lambda|c_4}{2}\varepsilon^{1/2}+c_5(\varepsilon^{\alpha}+\varepsilon^{1/2})\quad\forall 0<r\le\varepsilon. \end{align} $$
$$ \begin{align} &r^{1-\alpha}\left|\Phi_2(w,v)(r)+c_2r^{\alpha-1}\right|\notag\\ \le&|c_1|r+\frac{\alpha |\lambda|}{2}r|\log r| +\frac{(n-1)r}{2}\left|\int_r^{\varepsilon}\frac{\rho^{-1}v(\rho)}{w(\rho)}\,d\rho\right|+\frac{|\lambda|r}{2}\left|\int_0^r\frac{v(\rho)}{w(\rho)}\,d\rho\right|+\frac{r}{2} \left|\int_r^{\varepsilon}\frac{\rho^{-\alpha}v(\rho)^2}{w(\rho)}\,d\rho\right| \notag\\ \le&|c_1|\varepsilon+\frac{\alpha |\lambda|c_4}{2}\varepsilon^{1/2}+c_5(\varepsilon^{\alpha}+\varepsilon^{1/2})\quad\forall 0<r\le\varepsilon. \end{align} $$
Let
 $$ \begin{align*} \varepsilon_2=\min \left(\varepsilon_1,\frac{c_0}{30(|c_1|+1)},\left(\frac{c_0}{30c_5}\right)^{\frac{1}{\alpha}},\frac{c_0^2}{900(\alpha|\lambda|c_4+c_5)^2}\right) \end{align*} $$
$$ \begin{align*} \varepsilon_2=\min \left(\varepsilon_1,\frac{c_0}{30(|c_1|+1)},\left(\frac{c_0}{30c_5}\right)^{\frac{1}{\alpha}},\frac{c_0^2}{900(\alpha|\lambda|c_4+c_5)^2}\right) \end{align*} $$
and
![]() $\varepsilon \in (0,\varepsilon _2)$
. Then, by (2.15),
$\varepsilon \in (0,\varepsilon _2)$
. Then, by (2.15),
 $$ \begin{align} &r^{1-\alpha}\left|\Phi_2(w,v)(r)+c_2r^{\alpha-1}\right|\le c_0/10\quad\forall 0<r\le\varepsilon\notag\\ \Rightarrow\quad&\|r^{1-\alpha}(\Phi_2(w,v)(r)+c_2r^{\alpha-1})\|_{L^{\infty}\left([0, \varepsilon]\right)}\le c_0/10. \end{align} $$
$$ \begin{align} &r^{1-\alpha}\left|\Phi_2(w,v)(r)+c_2r^{\alpha-1}\right|\le c_0/10\quad\forall 0<r\le\varepsilon\notag\\ \Rightarrow\quad&\|r^{1-\alpha}(\Phi_2(w,v)(r)+c_2r^{\alpha-1})\|_{L^{\infty}\left([0, \varepsilon]\right)}\le c_0/10. \end{align} $$
Hence,
![]() $\Phi ({\mathcal D}_{\varepsilon })\subset {\mathcal D}_{\varepsilon }$
. Let
$\Phi ({\mathcal D}_{\varepsilon })\subset {\mathcal D}_{\varepsilon }$
. Let
![]() $(w_1,v_1), (w_2,v_2)\in {\mathcal D}_{\varepsilon }$
,
$(w_1,v_1), (w_2,v_2)\in {\mathcal D}_{\varepsilon }$
,
![]() $0<\varepsilon <\varepsilon _2$
,
$0<\varepsilon <\varepsilon _2$
,
![]() $\delta _1=\|(w_1,v_1)-(w_2,v_2)\|_{{\mathcal X}_\varepsilon }$
. Then
$\delta _1=\|(w_1,v_1)-(w_2,v_2)\|_{{\mathcal X}_\varepsilon }$
. Then
and
Now
 $$ \begin{align} |\Phi_1(w_1,v_1)(r)-\Phi_1(w_2,v_2)(r)|\le&\int_0^r|v_1(\rho)-v_2(\rho)|\,d\rho\notag\\ \le&\|r^{1-\alpha}(v_1(r)-v_2(r))\|_{L^{\infty}\left([0, \varepsilon]\right)}\int_0^r\rho^{\alpha-1}\,d\rho\notag\\ \le&(\delta_1/\alpha)\varepsilon^{\alpha}\quad\forall 0<r\le\varepsilon, \end{align} $$
$$ \begin{align} |\Phi_1(w_1,v_1)(r)-\Phi_1(w_2,v_2)(r)|\le&\int_0^r|v_1(\rho)-v_2(\rho)|\,d\rho\notag\\ \le&\|r^{1-\alpha}(v_1(r)-v_2(r))\|_{L^{\infty}\left([0, \varepsilon]\right)}\int_0^r\rho^{\alpha-1}\,d\rho\notag\\ \le&(\delta_1/\alpha)\varepsilon^{\alpha}\quad\forall 0<r\le\varepsilon, \end{align} $$
and by (2.11), (2.18), and (2.19), for any
![]() $0<r\le \varepsilon $
,
$0<r\le \varepsilon $
,
 $$ \begin{align} &r\left|\int_r^{\varepsilon}\frac{\rho^{-1}v_1(\rho)}{w_1(\rho)}\,d\rho-\int_r^{\varepsilon}\frac{\rho^{-1}v_2(\rho)}{w_2(\rho)}\,d\rho\right|\notag\\ \le& r\int_r^{\varepsilon}\frac{\rho^{-1}|v_1(\rho)-v_2(\rho)|}{w_1(\rho)}\,d\rho +r\int_r^{\varepsilon}\rho^{-1}|v_2(\rho)|\left|\frac{1}{w_1(\rho)}-\frac{1}{w_2(\rho)}\right|\,d\rho\notag\\ \le&\frac{10\|\rho^{1-\alpha}|v_1-v_2|(\rho)\|_{L^{\infty}\left([0, \varepsilon]\right)}r}{9c_0}\int_r^{\varepsilon}\rho^{\alpha-2}\,d\rho\notag\\ &\quad +\frac{100c_3\|w_1-w_2\|_{L^{\infty}\left([0, \varepsilon]\right)}r}{81c_0^2} \int_r^{\varepsilon}\rho^{\alpha-2}\,d\rho \notag\\ \le&\left\{\begin{aligned} &\left(\frac{10}{9c_0|\alpha -1|}+\frac{100c_3}{81c_0^2|\alpha -1|}\right)\delta_1r(r^{\alpha-1}+\varepsilon^{\alpha-1}),\quad\mbox{ if }n\ne 4\\ &\left(\frac{10}{9c_0}+\frac{100c_3}{81c_0^2}\right)\delta_1r|\log r|,\qquad\qquad\qquad\qquad\,\mbox{ if }n=4 \end{aligned} \right.\notag\\ \le&\left\{\begin{aligned} &\frac{c_6\delta_1\varepsilon^{\alpha}}{|\alpha -1|},\qquad\mbox{ if }n\ne 4,\\ &c_4c_6\delta_1\varepsilon^{1/2},\quad\mbox{ if }n=4, \end{aligned} \right. \end{align} $$
$$ \begin{align} &r\left|\int_r^{\varepsilon}\frac{\rho^{-1}v_1(\rho)}{w_1(\rho)}\,d\rho-\int_r^{\varepsilon}\frac{\rho^{-1}v_2(\rho)}{w_2(\rho)}\,d\rho\right|\notag\\ \le& r\int_r^{\varepsilon}\frac{\rho^{-1}|v_1(\rho)-v_2(\rho)|}{w_1(\rho)}\,d\rho +r\int_r^{\varepsilon}\rho^{-1}|v_2(\rho)|\left|\frac{1}{w_1(\rho)}-\frac{1}{w_2(\rho)}\right|\,d\rho\notag\\ \le&\frac{10\|\rho^{1-\alpha}|v_1-v_2|(\rho)\|_{L^{\infty}\left([0, \varepsilon]\right)}r}{9c_0}\int_r^{\varepsilon}\rho^{\alpha-2}\,d\rho\notag\\ &\quad +\frac{100c_3\|w_1-w_2\|_{L^{\infty}\left([0, \varepsilon]\right)}r}{81c_0^2} \int_r^{\varepsilon}\rho^{\alpha-2}\,d\rho \notag\\ \le&\left\{\begin{aligned} &\left(\frac{10}{9c_0|\alpha -1|}+\frac{100c_3}{81c_0^2|\alpha -1|}\right)\delta_1r(r^{\alpha-1}+\varepsilon^{\alpha-1}),\quad\mbox{ if }n\ne 4\\ &\left(\frac{10}{9c_0}+\frac{100c_3}{81c_0^2}\right)\delta_1r|\log r|,\qquad\qquad\qquad\qquad\,\mbox{ if }n=4 \end{aligned} \right.\notag\\ \le&\left\{\begin{aligned} &\frac{c_6\delta_1\varepsilon^{\alpha}}{|\alpha -1|},\qquad\mbox{ if }n\ne 4,\\ &c_4c_6\delta_1\varepsilon^{1/2},\quad\mbox{ if }n=4, \end{aligned} \right. \end{align} $$
where
 $$ \begin{align*} c_6=\frac{20}{9c_0}+\frac{200c_3}{81c_0^2}, \end{align*} $$
$$ \begin{align*} c_6=\frac{20}{9c_0}+\frac{200c_3}{81c_0^2}, \end{align*} $$
 $$ \begin{align} &r\left|\int_0^r\frac{v_1(\rho)}{w_1(\rho)}\,d\rho-\int_0^r\frac{v_2(\rho)}{w_2(\rho)}\,d\rho\right|\notag\\ \le& r\int_0^r\frac{|v_1(\rho)-v_2(\rho)|}{w_1(\rho)}\,d\rho +r\int_0^r|v_2(\rho)|\left|\frac{1}{w_1(\rho)}-\frac{1}{w_2(\rho)}\right|\,d\rho\notag\\ \le&\frac{10\|\rho^{1-\alpha}|v_1-v_2|(\rho)\|_{L^{\infty}\left([0, \varepsilon]\right)}r}{9c_0}\int_0^r\rho^{\alpha-1}\,d\rho \notag\\ &\quad +\frac{100c_3\|w_1-w_2\|_{L^{\infty}\left([0, \varepsilon]\right)}r}{81c_0^2} \int_0^r\rho^{\alpha-1}\,d\rho\notag\\ =&\left(\frac{10}{9c_0\alpha}+\frac{100c_3}{81c_0^2\alpha}\right)\delta_1r^{\alpha+1} \le \frac{c_6\delta_1\varepsilon^{\alpha+1}}{\alpha} \end{align} $$
$$ \begin{align} &r\left|\int_0^r\frac{v_1(\rho)}{w_1(\rho)}\,d\rho-\int_0^r\frac{v_2(\rho)}{w_2(\rho)}\,d\rho\right|\notag\\ \le& r\int_0^r\frac{|v_1(\rho)-v_2(\rho)|}{w_1(\rho)}\,d\rho +r\int_0^r|v_2(\rho)|\left|\frac{1}{w_1(\rho)}-\frac{1}{w_2(\rho)}\right|\,d\rho\notag\\ \le&\frac{10\|\rho^{1-\alpha}|v_1-v_2|(\rho)\|_{L^{\infty}\left([0, \varepsilon]\right)}r}{9c_0}\int_0^r\rho^{\alpha-1}\,d\rho \notag\\ &\quad +\frac{100c_3\|w_1-w_2\|_{L^{\infty}\left([0, \varepsilon]\right)}r}{81c_0^2} \int_0^r\rho^{\alpha-1}\,d\rho\notag\\ =&\left(\frac{10}{9c_0\alpha}+\frac{100c_3}{81c_0^2\alpha}\right)\delta_1r^{\alpha+1} \le \frac{c_6\delta_1\varepsilon^{\alpha+1}}{\alpha} \end{align} $$
and
 $$ \begin{align} &r\left|\int_r^{\varepsilon}\frac{\rho^{-\alpha}v_1(\rho)^2}{w_1(\rho)}\,d\rho-\int_r^{\varepsilon}\frac{\rho^{-\alpha}v_2(\rho)^2}{w_2(\rho)}\,d\rho\right|\notag\\ \le& r\int_r^{\varepsilon}\frac{\rho^{-\alpha}|v_1(\rho)-v_2(\rho)|(|v_1(\rho)|+|v_2(\rho)|)}{w_1(\rho)}\,d\rho\notag\\ &\quad+r\int_r^{\varepsilon}\rho^{-\alpha}|v_2(\rho)|^2\left|\frac{1}{w_1(\rho)}-\frac{1}{w_2(\rho)}\right|\,d\rho\notag\\ \le&\frac{20c_3\|\rho^{1-\alpha}|v_1-v_2|(\rho)\|_{L^{\infty}\left([0, \varepsilon]\right)}r}{9c_0}\int_r^{\varepsilon}\rho^{\alpha-2}\,d\rho\notag\\ &\quad+\frac{100c_3^2\|w_1-w_2\|_{L^{\infty}\left([0, \varepsilon]\right)}r}{81c_0^2} \int_r^{\varepsilon}\rho^{\alpha-2}\,d\rho \notag\\ \le&\left\{\begin{aligned} &\left(\frac{20c_3}{9c_0|\alpha -1|}+\frac{100c_3^2}{81c_0^2|\alpha -1|}\right)\delta_1r(r^{\alpha-1}+\varepsilon^{\alpha-1}),\quad\mbox{ if }n\ne 4\\ &\left(\frac{20c_3}{9c_0}+\frac{100c_3^2}{81c_0^2}\right)\delta_1r|\log r|,\qquad\qquad\qquad\qquad\,\mbox{if }n=4 \end{aligned} \right.\notag\\ \le&\left\{\begin{aligned} &\frac{2c_3c_6\delta_1\varepsilon^{\alpha}}{|\alpha -1|},\qquad\,\,\mbox{ if }n\ne 4,\\ &2c_3c_4c_6\delta_1\varepsilon^{1/2},\quad\mbox{ if }n=4. \end{aligned} \right. \end{align} $$
$$ \begin{align} &r\left|\int_r^{\varepsilon}\frac{\rho^{-\alpha}v_1(\rho)^2}{w_1(\rho)}\,d\rho-\int_r^{\varepsilon}\frac{\rho^{-\alpha}v_2(\rho)^2}{w_2(\rho)}\,d\rho\right|\notag\\ \le& r\int_r^{\varepsilon}\frac{\rho^{-\alpha}|v_1(\rho)-v_2(\rho)|(|v_1(\rho)|+|v_2(\rho)|)}{w_1(\rho)}\,d\rho\notag\\ &\quad+r\int_r^{\varepsilon}\rho^{-\alpha}|v_2(\rho)|^2\left|\frac{1}{w_1(\rho)}-\frac{1}{w_2(\rho)}\right|\,d\rho\notag\\ \le&\frac{20c_3\|\rho^{1-\alpha}|v_1-v_2|(\rho)\|_{L^{\infty}\left([0, \varepsilon]\right)}r}{9c_0}\int_r^{\varepsilon}\rho^{\alpha-2}\,d\rho\notag\\ &\quad+\frac{100c_3^2\|w_1-w_2\|_{L^{\infty}\left([0, \varepsilon]\right)}r}{81c_0^2} \int_r^{\varepsilon}\rho^{\alpha-2}\,d\rho \notag\\ \le&\left\{\begin{aligned} &\left(\frac{20c_3}{9c_0|\alpha -1|}+\frac{100c_3^2}{81c_0^2|\alpha -1|}\right)\delta_1r(r^{\alpha-1}+\varepsilon^{\alpha-1}),\quad\mbox{ if }n\ne 4\\ &\left(\frac{20c_3}{9c_0}+\frac{100c_3^2}{81c_0^2}\right)\delta_1r|\log r|,\qquad\qquad\qquad\qquad\,\mbox{if }n=4 \end{aligned} \right.\notag\\ \le&\left\{\begin{aligned} &\frac{2c_3c_6\delta_1\varepsilon^{\alpha}}{|\alpha -1|},\qquad\,\,\mbox{ if }n\ne 4,\\ &2c_3c_4c_6\delta_1\varepsilon^{1/2},\quad\mbox{ if }n=4. \end{aligned} \right. \end{align} $$
where
 $$ \begin{align*} c_7=\left\{\begin{aligned} &c_6\left(\frac{n(1+c_3)}{|\alpha -1|}+\frac{|\lambda|}{\alpha}\right),\quad\,\,\,\mbox{ if }n \ne 4,\\ &c_6\left(nc_4(1+c_3)+\frac{|\lambda|}{\alpha}\right),\quad\mbox{ if }n=4. \end{aligned} \right. \end{align*} $$
$$ \begin{align*} c_7=\left\{\begin{aligned} &c_6\left(\frac{n(1+c_3)}{|\alpha -1|}+\frac{|\lambda|}{\alpha}\right),\quad\,\,\,\mbox{ if }n \ne 4,\\ &c_6\left(nc_4(1+c_3)+\frac{|\lambda|}{\alpha}\right),\quad\mbox{ if }n=4. \end{aligned} \right. \end{align*} $$
Let
and
![]() $0<\varepsilon <\varepsilon _3$
. By (2.20) and (2.24),
$0<\varepsilon <\varepsilon _3$
. By (2.20) and (2.24),
Hence,
![]() $\Phi $
is a contraction map on
$\Phi $
is a contraction map on
![]() ${\mathcal D}_{\varepsilon }$
. Therefore, by the contraction map theorem, there exists a unique fixed point
${\mathcal D}_{\varepsilon }$
. Therefore, by the contraction map theorem, there exists a unique fixed point
![]() $(w,v)=\Phi (w,v)$
in
$(w,v)=\Phi (w,v)$
in
![]() ${\mathcal D}_{\varepsilon }$
. Thus,
${\mathcal D}_{\varepsilon }$
. Thus,
 $$ \begin{align} \left\{\begin{aligned} w(r)=\ &c_0+\int_0^r v(\rho)\,d\rho,\\ v(r)=&-c_2r^{\alpha-1}+c_1r^{\alpha}+\frac{\alpha\lambda}{2}r^{\alpha}\log r +r^{\alpha}\left\{\frac{(n-1)}{2}\int_r^{\varepsilon}\frac{\rho^{-1}v(\rho)}{w(\rho)}\,d\rho \right.\\ &\quad \left.-\frac{\lambda}{2}\int_0^r\frac{v(\rho)}{w(\rho)}\,d\rho-\frac{1}{2} \int_r^{\varepsilon}\frac{\rho^{-\alpha}v(\rho)^2}{w(\rho)}\,d\rho\right\}. \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{\begin{aligned} w(r)=\ &c_0+\int_0^r v(\rho)\,d\rho,\\ v(r)=&-c_2r^{\alpha-1}+c_1r^{\alpha}+\frac{\alpha\lambda}{2}r^{\alpha}\log r +r^{\alpha}\left\{\frac{(n-1)}{2}\int_r^{\varepsilon}\frac{\rho^{-1}v(\rho)}{w(\rho)}\,d\rho \right.\\ &\quad \left.-\frac{\lambda}{2}\int_0^r\frac{v(\rho)}{w(\rho)}\,d\rho-\frac{1}{2} \int_r^{\varepsilon}\frac{\rho^{-\alpha}v(\rho)^2}{w(\rho)}\,d\rho\right\}. \end{aligned} \right. \end{align} $$
By (2.26),
![]() $v(r)=w_r(r)$
for any
$v(r)=w_r(r)$
for any
![]() $0<r\le \varepsilon $
and
$0<r\le \varepsilon $
and
![]() $w\in C^2((0,\varepsilon ];{\mathbb {R}}^+)\cap C([0,\varepsilon ],{\mathbb {R}}^+)$
satisfies (2.2) and (2.4). Hence, w satisfies (2.1). By (2.4) and (2.12)–(2.14), we get (2.5) and the proposition follows.
$w\in C^2((0,\varepsilon ];{\mathbb {R}}^+)\cap C([0,\varepsilon ],{\mathbb {R}}^+)$
satisfies (2.2) and (2.4). Hence, w satisfies (2.1). By (2.4) and (2.12)–(2.14), we get (2.5) and the proposition follows.
By an argument similar to the proof of Proposition 2.1 , we have the following result.
Proposition Let
![]() $n\in {\mathbb Z}^+$
,
$n\in {\mathbb Z}^+$
,
![]() $n>4$
,
$n>4$
,
![]() $\alpha =\sqrt {n}-1$
,
$\alpha =\sqrt {n}-1$
,
![]() $\lambda , c_1\in {\mathbb {R}}$
,
$\lambda , c_1\in {\mathbb {R}}$
,
![]() $c_0>0$
, and let
$c_0>0$
, and let
![]() $c_2$
be given by (1.17). Then there exists a constant
$c_2$
be given by (1.17). Then there exists a constant
![]() $0<\varepsilon <1$
such that (2.1) has a unique solution
$0<\varepsilon <1$
such that (2.1) has a unique solution
![]() ${w\in C^2((0,\varepsilon ];{\mathbb {R}}^+)\cap C([0,\varepsilon ];{\mathbb {R}}^+)}$
in
${w\in C^2((0,\varepsilon ];{\mathbb {R}}^+)\cap C([0,\varepsilon ];{\mathbb {R}}^+)}$
in
![]() $(0,\varepsilon ]$
which satisfies (2.2) and
$(0,\varepsilon ]$
which satisfies (2.2) and
 $$ \begin{align} w_r(r)=&-c_2r^{\alpha-1}+c_1r^{\alpha}+\frac{\alpha\lambda}{2}r^{\alpha}\log r +r^{\alpha}\left\{-\frac{(n-1)}{2}\int_0^r\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho \right.\notag\\ &\quad \left.-\frac{\lambda}{2}\int_0^r\frac{w_r(\rho)}{w(\rho)}\,d\rho+\frac{1}{2} \int_0^r\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho\right\}\qquad\qquad\forall 0<r\le\varepsilon. \end{align} $$
$$ \begin{align} w_r(r)=&-c_2r^{\alpha-1}+c_1r^{\alpha}+\frac{\alpha\lambda}{2}r^{\alpha}\log r +r^{\alpha}\left\{-\frac{(n-1)}{2}\int_0^r\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho \right.\notag\\ &\quad \left.-\frac{\lambda}{2}\int_0^r\frac{w_r(\rho)}{w(\rho)}\,d\rho+\frac{1}{2} \int_0^r\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho\right\}\qquad\qquad\forall 0<r\le\varepsilon. \end{align} $$
Moreover, (2.5) holds.
Corollary Let
![]() $2\le n\in {\mathbb Z}^+$
,
$2\le n\in {\mathbb Z}^+$
,
![]() $\alpha =\sqrt {n}-1$
,
$\alpha =\sqrt {n}-1$
,
![]() $\lambda , c_1\in {\mathbb {R}}$
,
$\lambda , c_1\in {\mathbb {R}}$
,
![]() $c_0>0$
, and let
$c_0>0$
, and let
![]() $c_2$
be given by (1.17). Then there exists a constant
$c_2$
be given by (1.17). Then there exists a constant
![]() $0<\varepsilon <1$
such that (1.10) has infinitely many solutions
$0<\varepsilon <1$
such that (1.10) has infinitely many solutions
![]() $h\in C^2((0,\varepsilon ])$
in
$h\in C^2((0,\varepsilon ])$
in
![]() $(0,\varepsilon ]$
which satisfies (1.11). Moreover, (1.10) has a unique solution
$(0,\varepsilon ]$
which satisfies (1.11). Moreover, (1.10) has a unique solution
![]() $h\in C^2((0,\varepsilon ])$
in
$h\in C^2((0,\varepsilon ])$
in
![]() $(0,\varepsilon ]$
which satisfies (1.11) and (2.4) with w being given by (1.12). Moreover, (2.5) holds.
$(0,\varepsilon ]$
which satisfies (1.11) and (2.4) with w being given by (1.12). Moreover, (2.5) holds.
Corollary Let
![]() $n\in {\mathbb Z}^+$
,
$n\in {\mathbb Z}^+$
,
![]() $n>4$
,
$n>4$
,
![]() $\alpha =\sqrt {n}-1$
,
$\alpha =\sqrt {n}-1$
,
![]() $\lambda , c_1\in {\mathbb {R}}$
,
$\lambda , c_1\in {\mathbb {R}}$
,
![]() $c_0>0$
, and let
$c_0>0$
, and let
![]() $c_2$
be given by (1.17). Then there exists a constant
$c_2$
be given by (1.17). Then there exists a constant
![]() $0<\varepsilon <1$
such that (1.10) has a unique solution
$0<\varepsilon <1$
such that (1.10) has a unique solution
![]() $h\in C^2((0,\varepsilon ])$
in
$h\in C^2((0,\varepsilon ])$
in
![]() $(0,\varepsilon ]$
which satisfies (1.11) and (2.27) with w being given by (1.12). Moreover, (2.5) holds.
$(0,\varepsilon ]$
which satisfies (1.11) and (2.27) with w being given by (1.12). Moreover, (2.5) holds.
Proposition Let
![]() $n\in {\mathbb Z}^+$
,
$n\in {\mathbb Z}^+$
,
![]() $n>4$
,
$n>4$
,
![]() $\alpha =\sqrt {n}-1$
,
$\alpha =\sqrt {n}-1$
,
![]() $\lambda , c_1\in {\mathbb {R}}$
,
$\lambda , c_1\in {\mathbb {R}}$
,
![]() $c_0>0$
, and let
$c_0>0$
, and let
![]() $c_2$
be given by (1.17). Then there exists a constant
$c_2$
be given by (1.17). Then there exists a constant
![]() $0<\varepsilon <1$
such that (1.10) has a unique solution
$0<\varepsilon <1$
such that (1.10) has a unique solution
![]() $h\in C^2((0,\varepsilon ])$
in
$h\in C^2((0,\varepsilon ])$
in
![]() $(0,\varepsilon ]$
which satisfies (1.11) and (1.18) for some constant
$(0,\varepsilon ]$
which satisfies (1.11) and (1.18) for some constant
![]() $0<\delta _0<\varepsilon $
. Moreover, (1.19) and (2.5) hold with w being given by (1.12).
$0<\delta _0<\varepsilon $
. Moreover, (1.19) and (2.5) hold with w being given by (1.12).
Proof Since
![]() $n>4$
,
$n>4$
,
![]() $\alpha>1$
and
$\alpha>1$
and
![]() $c_2>0$
. Let w be given by (1.12). By Corollary 2.4, there exists a constant
$c_2>0$
. Let w be given by (1.12). By Corollary 2.4, there exists a constant
![]() $0<\varepsilon <1$
such that (1.10) has a unique solution
$0<\varepsilon <1$
such that (1.10) has a unique solution
![]() $h\in C^2((0,\varepsilon ])$
in
$h\in C^2((0,\varepsilon ])$
in
![]() $(0,\varepsilon ]$
which satisfies (1.11), (2.5), and (2.27). Let
$(0,\varepsilon ]$
which satisfies (1.11), (2.5), and (2.27). Let
 $$ \begin{align} 0<\delta_1<\min\left(\varepsilon,\frac{|c_2|}{2c_0},\frac{c_2^2}{2c_0}\right). \end{align} $$
$$ \begin{align} 0<\delta_1<\min\left(\varepsilon,\frac{|c_2|}{2c_0},\frac{c_2^2}{2c_0}\right). \end{align} $$
By (1.11) and (2.5), there exist constants
![]() $\delta _0\in (0,\varepsilon )$
and
$\delta _0\in (0,\varepsilon )$
and
![]() $c_8>0$
such that
$c_8>0$
such that
 $$ \begin{align} -\frac{c_2}{c_0}-\delta_1\le \frac{r^{1-\alpha}w_r(r)}{w(r)} \le -\frac{c_2}{c_0}+\delta_1\quad\forall 0<r\le\delta_0 \end{align} $$
$$ \begin{align} -\frac{c_2}{c_0}-\delta_1\le \frac{r^{1-\alpha}w_r(r)}{w(r)} \le -\frac{c_2}{c_0}+\delta_1\quad\forall 0<r\le\delta_0 \end{align} $$
and
 $$ \begin{align} \frac{c_2^2}{c_0}-\delta_1\le \frac{(r^{1-\alpha}w_r(r))^2}{w(r)} \le \frac{c_2^2}{c_0}+\delta_1\quad\forall 0<r\le\delta_0 \end{align} $$
$$ \begin{align} \frac{c_2^2}{c_0}-\delta_1\le \frac{(r^{1-\alpha}w_r(r))^2}{w(r)} \le \frac{c_2^2}{c_0}+\delta_1\quad\forall 0<r\le\delta_0 \end{align} $$
holds. Then, by (2.29) and (2.30),
 $$ \begin{align} &-\frac{(n-1)}{2}\int_0^r\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho-\frac{\lambda}{2}\int_0^r\frac{w_r(\rho)}{w(\rho)}\,d\rho+\frac{1}{2}\int_0^r\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho\notag\\ \le&\frac{(n-1)}{2}\left(\frac{c_2}{c_0}+\delta_1\right)\int_0^r\rho^{\alpha-2}\,d\rho +\frac{\lambda}{2}\left(\frac{c_2}{c_0}+\mbox{sign}\,(\lambda)\delta_1\right)\int_0^r\rho^{\alpha-1}\,d\rho\notag\\ &\quad +\frac{1}{2}\left(\frac{c_2^2}{c_0}+\delta_1\right)\int_0^r\rho^{\alpha-2}\,d\rho \notag\\ \le& \frac{c_2(n-1+c_2)}{2c_0(\alpha -1)}r^{\alpha -1}+\frac{\lambda c_2}{2c_0\alpha}r^{\alpha}+\frac{n\delta_1}{2(\alpha -1)}r^{\alpha -1}+\frac{|\lambda|\delta_1}{2\alpha}r^{\alpha}\quad\forall 0<r\le\delta_0 \end{align} $$
$$ \begin{align} &-\frac{(n-1)}{2}\int_0^r\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho-\frac{\lambda}{2}\int_0^r\frac{w_r(\rho)}{w(\rho)}\,d\rho+\frac{1}{2}\int_0^r\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho\notag\\ \le&\frac{(n-1)}{2}\left(\frac{c_2}{c_0}+\delta_1\right)\int_0^r\rho^{\alpha-2}\,d\rho +\frac{\lambda}{2}\left(\frac{c_2}{c_0}+\mbox{sign}\,(\lambda)\delta_1\right)\int_0^r\rho^{\alpha-1}\,d\rho\notag\\ &\quad +\frac{1}{2}\left(\frac{c_2^2}{c_0}+\delta_1\right)\int_0^r\rho^{\alpha-2}\,d\rho \notag\\ \le& \frac{c_2(n-1+c_2)}{2c_0(\alpha -1)}r^{\alpha -1}+\frac{\lambda c_2}{2c_0\alpha}r^{\alpha}+\frac{n\delta_1}{2(\alpha -1)}r^{\alpha -1}+\frac{|\lambda|\delta_1}{2\alpha}r^{\alpha}\quad\forall 0<r\le\delta_0 \end{align} $$
and
 $$ \begin{align} &-\frac{(n-1)}{2}\int_0^r\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho-\frac{\lambda}{2}\int_0^r\frac{w_r(\rho)}{w(\rho)}\,d\rho+\frac{1}{2}\int_0^r\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho\notag\\ \ge&\frac{(n-1)}{2}\left(\frac{c_2}{c_0}-\delta_1\right)\int_0^r\rho^{\alpha-2}\,d\rho +\frac{\lambda}{2}\left(\frac{c_2}{c_0}-\mbox{sign}\,(\lambda)\delta_1\right)\int_0^r\rho^{\alpha-1}\,d\rho\notag\\ &\quad +\frac{1}{2}\left(\frac{c_2^2}{c_0}-\delta_1\right)\int_0^r\rho^{\alpha-2}\,d\rho \notag\\ \ge& \frac{c_2(n-1+c_2)}{2c_0(\alpha -1)}r^{\alpha -1}+\frac{\lambda c_2}{2c_0\alpha}r^{\alpha}-\frac{n\delta_1}{2(\alpha -1)}r^{\alpha -1}-\frac{|\lambda|\delta_1}{2\alpha}r^{\alpha}\quad\forall 0<r\le\delta_0. \end{align} $$
$$ \begin{align} &-\frac{(n-1)}{2}\int_0^r\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho-\frac{\lambda}{2}\int_0^r\frac{w_r(\rho)}{w(\rho)}\,d\rho+\frac{1}{2}\int_0^r\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho\notag\\ \ge&\frac{(n-1)}{2}\left(\frac{c_2}{c_0}-\delta_1\right)\int_0^r\rho^{\alpha-2}\,d\rho +\frac{\lambda}{2}\left(\frac{c_2}{c_0}-\mbox{sign}\,(\lambda)\delta_1\right)\int_0^r\rho^{\alpha-1}\,d\rho\notag\\ &\quad +\frac{1}{2}\left(\frac{c_2^2}{c_0}-\delta_1\right)\int_0^r\rho^{\alpha-2}\,d\rho \notag\\ \ge& \frac{c_2(n-1+c_2)}{2c_0(\alpha -1)}r^{\alpha -1}+\frac{\lambda c_2}{2c_0\alpha}r^{\alpha}-\frac{n\delta_1}{2(\alpha -1)}r^{\alpha -1}-\frac{|\lambda|\delta_1}{2\alpha}r^{\alpha}\quad\forall 0<r\le\delta_0. \end{align} $$
Hence, by (1.11), (2.27), (2.31), and (2.32),
 $$ \begin{align} &w_r(r)=-c_2r^{\alpha-1}+c_1r^{\alpha}+\frac{\alpha\lambda}{2}r^{\alpha}\log r +\frac{c_2(n-1+c_2)}{2c_0(\alpha -1)}r^{2\alpha -1}+o(1)(r^{2\alpha-1}) \\ \Rightarrow\quad&r^{\alpha}h(r)=c_0-\frac{c_2}{\alpha}r^{\alpha}+\left(\frac{c_1}{\alpha+1}-\frac{\alpha\lambda}{2(\alpha +1)^2}\right)r^{\alpha +1}+\frac{\alpha\lambda}{2\alpha +2}r^{\alpha +1}\log r\notag\\ &\qquad +\frac{c_2(n-1+c_2)}{4c_0\alpha (\alpha -1)}r^{2\alpha}+o(1)r^{2\alpha}\quad\forall 0<r\le\delta_0\notag \end{align} $$
$$ \begin{align} &w_r(r)=-c_2r^{\alpha-1}+c_1r^{\alpha}+\frac{\alpha\lambda}{2}r^{\alpha}\log r +\frac{c_2(n-1+c_2)}{2c_0(\alpha -1)}r^{2\alpha -1}+o(1)(r^{2\alpha-1}) \\ \Rightarrow\quad&r^{\alpha}h(r)=c_0-\frac{c_2}{\alpha}r^{\alpha}+\left(\frac{c_1}{\alpha+1}-\frac{\alpha\lambda}{2(\alpha +1)^2}\right)r^{\alpha +1}+\frac{\alpha\lambda}{2\alpha +2}r^{\alpha +1}\log r\notag\\ &\qquad +\frac{c_2(n-1+c_2)}{4c_0\alpha (\alpha -1)}r^{2\alpha}+o(1)r^{2\alpha}\quad\forall 0<r\le\delta_0\notag \end{align} $$
and (1.18) follows. Since
by (1.18) and (2.33), we get (1.19).
Suppose
![]() $h_1\in C^2((0,\varepsilon ))$
is another solution of (1.10) which satisfies (1.11) and
$h_1\in C^2((0,\varepsilon ))$
is another solution of (1.10) which satisfies (1.11) and
 $$ \begin{align} h_1(r)=&\frac{1}{r^{\alpha}}\left\{c_0-\frac{c_2}{\alpha}r^{\alpha}+\left(\frac{c_1}{\alpha+1}-\frac{\alpha\lambda}{2(\alpha +1)^2}\right)r^{\alpha +1}+\frac{\alpha\lambda}{2\alpha +2}r^{\alpha +1}\log r \right.\notag\\ &\quad +\frac{c_2(n-1+c_2)}{4c_0\alpha (\alpha -1)}r^{2\alpha}+\left.o(1)r^{2\alpha}\right\}\quad\forall 0<r\le \delta_0. \end{align} $$
$$ \begin{align} h_1(r)=&\frac{1}{r^{\alpha}}\left\{c_0-\frac{c_2}{\alpha}r^{\alpha}+\left(\frac{c_1}{\alpha+1}-\frac{\alpha\lambda}{2(\alpha +1)^2}\right)r^{\alpha +1}+\frac{\alpha\lambda}{2\alpha +2}r^{\alpha +1}\log r \right.\notag\\ &\quad +\frac{c_2(n-1+c_2)}{4c_0\alpha (\alpha -1)}r^{2\alpha}+\left.o(1)r^{2\alpha}\right\}\quad\forall 0<r\le \delta_0. \end{align} $$
Let
![]() $w_1(r)=r^{\alpha }h_1(r)$
. Then
$w_1(r)=r^{\alpha }h_1(r)$
. Then
![]() $w_1$
satisfies (2.3). Integrating equation (2.3) for
$w_1$
satisfies (2.3). Integrating equation (2.3) for
![]() $w_1$
over
$w_1$
over
![]() $(0,r)$
, we get
$(0,r)$
, we get
 $$ \begin{align} w_{1,r}(r)=&-c_2r^{\alpha-1}+c_1'r^{\alpha}+\frac{\alpha\lambda}{2}r^{\alpha}\log r +r^{\alpha}\left\{-\frac{(n-1)}{2}\int_0^r\frac{\rho^{-1}w_{1,r}(\rho)}{w_1(\rho)}\,d\rho \right.\notag\\ &\quad \left.-\frac{\lambda}{2}\int_0^r\frac{w_{1,r}(\rho)}{w_1(\rho)}\,d\rho+\frac{1}{2} \int_0^r\frac{\rho^{-\alpha}w_{1,r}(\rho)^2}{w_1(\rho)}\,d\rho\right\}\qquad\qquad\forall 0<r\le\varepsilon \end{align} $$
$$ \begin{align} w_{1,r}(r)=&-c_2r^{\alpha-1}+c_1'r^{\alpha}+\frac{\alpha\lambda}{2}r^{\alpha}\log r +r^{\alpha}\left\{-\frac{(n-1)}{2}\int_0^r\frac{\rho^{-1}w_{1,r}(\rho)}{w_1(\rho)}\,d\rho \right.\notag\\ &\quad \left.-\frac{\lambda}{2}\int_0^r\frac{w_{1,r}(\rho)}{w_1(\rho)}\,d\rho+\frac{1}{2} \int_0^r\frac{\rho^{-\alpha}w_{1,r}(\rho)^2}{w_1(\rho)}\,d\rho\right\}\qquad\qquad\forall 0<r\le\varepsilon \end{align} $$
for some constant
![]() $c_1'\in {\mathbb {R}}$
. By (2.36) and a similar argument as before, we get
$c_1'\in {\mathbb {R}}$
. By (2.36) and a similar argument as before, we get
 $$ \begin{align} h_1(r)=&\frac{1}{r^{\alpha}}\left\{c_0-\frac{c_2}{\alpha}r^{\alpha}+\left(\frac{c_1'}{\alpha+1}-\frac{\alpha\lambda}{2(\alpha +1)^2}\right)r^{\alpha +1}+\frac{\alpha\lambda}{2\alpha +2}r^{\alpha +1}\log r \right.\notag\\ &\quad +\frac{c_2(n-1+c_2)}{4c_0\alpha (\alpha -1)}r^{2\alpha}+\left.o(1)r^{2\alpha}\right\}\quad\forall 0<r\le \delta_0. \end{align} $$
$$ \begin{align} h_1(r)=&\frac{1}{r^{\alpha}}\left\{c_0-\frac{c_2}{\alpha}r^{\alpha}+\left(\frac{c_1'}{\alpha+1}-\frac{\alpha\lambda}{2(\alpha +1)^2}\right)r^{\alpha +1}+\frac{\alpha\lambda}{2\alpha +2}r^{\alpha +1}\log r \right.\notag\\ &\quad +\frac{c_2(n-1+c_2)}{4c_0\alpha (\alpha -1)}r^{2\alpha}+\left.o(1)r^{2\alpha}\right\}\quad\forall 0<r\le \delta_0. \end{align} $$
Hence, both w and
![]() $w_1$
satisfy (2.27). Then, by Proposition 2.2,
$w_1$
satisfy (2.27). Then, by Proposition 2.2,
![]() $w\equiv w_1$
on
$w\equiv w_1$
on
![]() $[0,\varepsilon ]$
. Thus,
$[0,\varepsilon ]$
. Thus,
![]() $h=h_1$
on
$h=h_1$
on
![]() $[0,\varepsilon ]$
and the solution h is unique.
$[0,\varepsilon ]$
and the solution h is unique.
Proposition Let
![]() $n\in \{2,3,4\}$
,
$n\in \{2,3,4\}$
,
![]() $\alpha =\sqrt {n}-1$
,
$\alpha =\sqrt {n}-1$
,
![]() $\lambda , c_1\in {\mathbb {R}}$
,
$\lambda , c_1\in {\mathbb {R}}$
,
![]() $c_0>0$
, and let
$c_0>0$
, and let
![]() $c_2$
be given by (1.17). Let
$c_2$
be given by (1.17). Let
![]() $0<\varepsilon <1$
, and let
$0<\varepsilon <1$
, and let
![]() $h\in C^2((0,\varepsilon ])$
be the unique solution of (1.10) in
$h\in C^2((0,\varepsilon ])$
be the unique solution of (1.10) in
![]() $(0,\varepsilon ]$
given by Corollary 2.3, which satisfies (1.11), (2.4), and (2.5) with w being given by (1.12). Then there exists a constant
$(0,\varepsilon ]$
given by Corollary 2.3, which satisfies (1.11), (2.4), and (2.5) with w being given by (1.12). Then there exists a constant
![]() $0<\delta _0<\varepsilon $
such that (1.20) and (1.21) hold.
$0<\delta _0<\varepsilon $
such that (1.20) and (1.21) hold.
Proof Note that
![]() $\alpha <1$
,
$\alpha <1$
,
![]() $1/(1-\alpha )\le 4$
, and
$1/(1-\alpha )\le 4$
, and
![]() $c_2<0$
when
$c_2<0$
when
![]() $n=2$
or
$n=2$
or
![]() $3$
, and
$3$
, and
![]() $\alpha =1$
and
$\alpha =1$
and
![]() ${c_2=0}$
, when
${c_2=0}$
, when
![]() $n=4$
. Let
$n=4$
. Let
![]() $\delta _1$
satisfy (2.28) when
$\delta _1$
satisfy (2.28) when
![]() $n=2,3$
and
$n=2,3$
and
![]() $0<\delta _1<\varepsilon $
when
$0<\delta _1<\varepsilon $
when
![]() $n=4$
. By (1.11) and (2.5), there exists a constant
$n=4$
. By (1.11) and (2.5), there exists a constant
![]() $0<\delta _0<\varepsilon $
such that (2.29) and (2.30) hold. Hence, by (2.29) and (2.30), for any
$0<\delta _0<\varepsilon $
such that (2.29) and (2.30) hold. Hence, by (2.29) and (2.30), for any
![]() $0<r<\delta _0$
,
$0<r<\delta _0$
,
 $$ \begin{align} &\frac{(n-1)}{2}\int_r^{\varepsilon}\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho-\frac{\lambda}{2}\int_0^r\frac{w_r(\rho)}{w(\rho)}\,d\rho-\frac{1}{2}\int_r^{\varepsilon}\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho\notag\\ \le&\frac{(n-1)}{2}\left(-\frac{c_2}{c_0}+\delta_1\right)\int_r^{\delta_0}\rho^{\alpha-2}\,d\rho +\frac{\lambda}{2}\left(\frac{c_2}{c_0}+\mbox{sign}\,(\lambda)\delta_1\right)\int_0^r\rho^{\alpha-1}\,d\rho \notag\\ &\quad -\frac{1}{2}\left(\frac{c_2^2}{c_0}-\delta_1\right)\int_r^{\delta_0}\rho^{\alpha-2}\,d\rho+c_8\notag\\ \le&\left\{\begin{aligned} &\begin{aligned} &-\frac{c_2(c_2+n-1)}{2c_0(1-\alpha)}(r^{\alpha -1}-\delta_0^{\alpha -1})+\frac{\lambda c_2}{2c_0\alpha}r^{\alpha}+\frac{n\delta_1}{2(1-\alpha)}(r^{\alpha -1}-\delta_0^{\alpha -1})\\ &\qquad +\frac{|\lambda|\delta_1}{2\alpha}r^{\alpha}+c_8 \end{aligned},\quad\mbox{ if }n=2,3\\ &\frac{n\delta_1}{2}(\log\delta_0-\log r)+\frac{|\lambda|\delta_1}{2}r+c_8,\qquad\,\,\mbox{ if } n=4 \end{aligned} \right. \end{align} $$
$$ \begin{align} &\frac{(n-1)}{2}\int_r^{\varepsilon}\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho-\frac{\lambda}{2}\int_0^r\frac{w_r(\rho)}{w(\rho)}\,d\rho-\frac{1}{2}\int_r^{\varepsilon}\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho\notag\\ \le&\frac{(n-1)}{2}\left(-\frac{c_2}{c_0}+\delta_1\right)\int_r^{\delta_0}\rho^{\alpha-2}\,d\rho +\frac{\lambda}{2}\left(\frac{c_2}{c_0}+\mbox{sign}\,(\lambda)\delta_1\right)\int_0^r\rho^{\alpha-1}\,d\rho \notag\\ &\quad -\frac{1}{2}\left(\frac{c_2^2}{c_0}-\delta_1\right)\int_r^{\delta_0}\rho^{\alpha-2}\,d\rho+c_8\notag\\ \le&\left\{\begin{aligned} &\begin{aligned} &-\frac{c_2(c_2+n-1)}{2c_0(1-\alpha)}(r^{\alpha -1}-\delta_0^{\alpha -1})+\frac{\lambda c_2}{2c_0\alpha}r^{\alpha}+\frac{n\delta_1}{2(1-\alpha)}(r^{\alpha -1}-\delta_0^{\alpha -1})\\ &\qquad +\frac{|\lambda|\delta_1}{2\alpha}r^{\alpha}+c_8 \end{aligned},\quad\mbox{ if }n=2,3\\ &\frac{n\delta_1}{2}(\log\delta_0-\log r)+\frac{|\lambda|\delta_1}{2}r+c_8,\qquad\,\,\mbox{ if } n=4 \end{aligned} \right. \end{align} $$
and
 $$ \begin{align} &\frac{(n-1)}{2}\int_r^{\varepsilon}\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho-\frac{\lambda}{2}\int_0^r\frac{w_r(\rho)}{w(\rho)}\,d\rho-\frac{1}{2}\int_r^{\varepsilon}\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho\notag\\ \ge&\frac{(n-1)}{2}\left(-\frac{c_2}{c_0}-\delta_1\right)\int_r^{\delta_0}\rho^{\alpha-2}\,d\rho +\frac{\lambda}{2}\left(\frac{c_2}{c_0}-\mbox{sign}\,(\lambda)\delta_1\right)\int_0^r\rho^{\alpha-1}\,d\rho \notag\\ &\quad -\frac{1}{2}\left(\frac{c_2^2}{c_0}+\delta_1\right)\int_r^{\delta_0}\rho^{\alpha-2}\,d\rho+c_8\notag\\ \ge&\left\{\begin{aligned} &\begin{aligned} &-\frac{c_2(c_2+n-1)}{2c_0(1-\alpha)}(r^{\alpha -1}-\delta_0^{\alpha -1})+\frac{\lambda c_2}{2c_0\alpha}r^{\alpha}-\frac{n\delta_1}{2(1-\alpha)}(r^{\alpha -1}-\delta_0^{\alpha -1})\\ &\qquad-\frac{|\lambda|\delta_1}{2\alpha}r^{\alpha}+c_8,\end{aligned} \,\mbox{ if }n=2,3,\\ &-\frac{n\delta_1}{2}(\log\delta_0-\log r)-\frac{|\lambda|\delta_1}{2}r+c_8,\quad\mbox{ if } n=4, \end{aligned} \right. \end{align} $$
$$ \begin{align} &\frac{(n-1)}{2}\int_r^{\varepsilon}\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho-\frac{\lambda}{2}\int_0^r\frac{w_r(\rho)}{w(\rho)}\,d\rho-\frac{1}{2}\int_r^{\varepsilon}\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho\notag\\ \ge&\frac{(n-1)}{2}\left(-\frac{c_2}{c_0}-\delta_1\right)\int_r^{\delta_0}\rho^{\alpha-2}\,d\rho +\frac{\lambda}{2}\left(\frac{c_2}{c_0}-\mbox{sign}\,(\lambda)\delta_1\right)\int_0^r\rho^{\alpha-1}\,d\rho \notag\\ &\quad -\frac{1}{2}\left(\frac{c_2^2}{c_0}+\delta_1\right)\int_r^{\delta_0}\rho^{\alpha-2}\,d\rho+c_8\notag\\ \ge&\left\{\begin{aligned} &\begin{aligned} &-\frac{c_2(c_2+n-1)}{2c_0(1-\alpha)}(r^{\alpha -1}-\delta_0^{\alpha -1})+\frac{\lambda c_2}{2c_0\alpha}r^{\alpha}-\frac{n\delta_1}{2(1-\alpha)}(r^{\alpha -1}-\delta_0^{\alpha -1})\\ &\qquad-\frac{|\lambda|\delta_1}{2\alpha}r^{\alpha}+c_8,\end{aligned} \,\mbox{ if }n=2,3,\\ &-\frac{n\delta_1}{2}(\log\delta_0-\log r)-\frac{|\lambda|\delta_1}{2}r+c_8,\quad\mbox{ if } n=4, \end{aligned} \right. \end{align} $$
where
 $$ \begin{align*} c_8=\frac{(n-1)}{2}\int_{\delta_0}^{\varepsilon}\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho -\frac{1}{2}\int_{\delta_0}^{\varepsilon}\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho. \end{align*} $$
$$ \begin{align*} c_8=\frac{(n-1)}{2}\int_{\delta_0}^{\varepsilon}\frac{\rho^{-1}w_r(\rho)}{w(\rho)}\,d\rho -\frac{1}{2}\int_{\delta_0}^{\varepsilon}\frac{\rho^{-\alpha}w_r(\rho)^2}{w(\rho)}\,d\rho. \end{align*} $$
Thus, by (1.11), (2.4), (2.38), and (2.39),
 $$ \begin{align} &w_r(r)=\left\{\begin{aligned} &-c_2r^{\alpha-1}-\frac{c_2(c_2+n-1)}{2c_0(1-\alpha)}r^{2\alpha-1}+o(1)(r^{2\alpha-1})\quad\forall 0<r\le\delta_0,\quad\mbox{ if }n=2,3,\\ &\frac{\lambda}{2}r\log r+o(1)(r|\log r|)\qquad\qquad\qquad\qquad\quad\forall 0<r\le\delta_0,\quad\mbox{ if }n=4, \end{aligned} \right. \end{align} $$
$$ \begin{align} &w_r(r)=\left\{\begin{aligned} &-c_2r^{\alpha-1}-\frac{c_2(c_2+n-1)}{2c_0(1-\alpha)}r^{2\alpha-1}+o(1)(r^{2\alpha-1})\quad\forall 0<r\le\delta_0,\quad\mbox{ if }n=2,3,\\ &\frac{\lambda}{2}r\log r+o(1)(r|\log r|)\qquad\qquad\qquad\qquad\quad\forall 0<r\le\delta_0,\quad\mbox{ if }n=4, \end{aligned} \right. \end{align} $$
 $$ \begin{align} \Rightarrow\ \ &w(r)=r^{\alpha}h(r)=\left\{\begin{aligned} &c_0-\frac{c_2}{\alpha}r^{\alpha}-\frac{c_2(c_2+n-1)}{4c_0\alpha (1-\alpha)}r^{2\alpha}+o(1)r^{2\alpha}\!\quad\forall 0<r\le\delta_0, \quad\mbox{if }n=2,3,\\ &c_0+\frac{\lambda}{4}r^2\log r+o(1)r^2|\log r|\qquad\qquad\quad\ \ \forall 0<r\le\delta_0,\quad\mbox{if }n=4, \end{aligned} \right. \end{align} $$
$$ \begin{align} \Rightarrow\ \ &w(r)=r^{\alpha}h(r)=\left\{\begin{aligned} &c_0-\frac{c_2}{\alpha}r^{\alpha}-\frac{c_2(c_2+n-1)}{4c_0\alpha (1-\alpha)}r^{2\alpha}+o(1)r^{2\alpha}\!\quad\forall 0<r\le\delta_0, \quad\mbox{if }n=2,3,\\ &c_0+\frac{\lambda}{4}r^2\log r+o(1)r^2|\log r|\qquad\qquad\quad\ \ \forall 0<r\le\delta_0,\quad\mbox{if }n=4, \end{aligned} \right. \end{align} $$
and (1.20) follows. By (1.20), (2.34), and (2.40), we get (1.21) and the proposition follows.
3 Global existence and uniqueness of singular solutions
In this section, we will use a modification of the technique of Hsu [Reference Hsu9] to prove the global existence of infinitely many singular solutions of (1.10) and (1.11) in
![]() $(0,\infty )$
. We will also prove the uniqueness of the global singular solution of such equation in terms of its asymptotic behavior near the origin.
$(0,\infty )$
. We will also prove the uniqueness of the global singular solution of such equation in terms of its asymptotic behavior near the origin.
Lemma 3.1 Let
![]() $2\le n\in {\mathbb Z}^+$
,
$2\le n\in {\mathbb Z}^+$
,
![]() $\lambda \in \mathbb {R}$
, and
$\lambda \in \mathbb {R}$
, and
![]() $L>0$
. Suppose
$L>0$
. Suppose
![]() $h\in C^2((0,L))$
satisfies (1.10) in
$h\in C^2((0,L))$
satisfies (1.10) in
![]() $(0,L)$
. Then
$(0,L)$
. Then
 $$ \begin{align} h_r(r_1)=\frac{n-1}{r_1}+\lambda+\sqrt{\frac{h(r_1)}{h(r_2)}}\left(h_r(r_2)-\frac{n-1}{r_2}-\lambda\right)+\frac{(n-1)\sqrt{h(r_1)}}{2}\int_{r_2}^{r_1}\frac{h(\rho)+1}{\rho^2\sqrt{h(\rho)}}\,d\rho \end{align} $$
$$ \begin{align} h_r(r_1)=\frac{n-1}{r_1}+\lambda+\sqrt{\frac{h(r_1)}{h(r_2)}}\left(h_r(r_2)-\frac{n-1}{r_2}-\lambda\right)+\frac{(n-1)\sqrt{h(r_1)}}{2}\int_{r_2}^{r_1}\frac{h(\rho)+1}{\rho^2\sqrt{h(\rho)}}\,d\rho \end{align} $$
holds for any
![]() $0<r_2<r_1<L$
.
$0<r_2<r_1<L$
.
Proof By (1.10),
 $$ \begin{align*} (h^{-1/2}h_r)_r=\ &\frac{(n-1)(h-1)}{2r^2h^{1/2}}-\frac{(n-1+\lambda r)h_r}{2rh^{3/2}}\quad\forall r>0\\\Rightarrow\ h_r(r_1)=\ &\sqrt{h(r_1)}\left\{\frac{h_r(r_2)}{\sqrt{h(r_2)}}+\frac{(n-1)}{2} \int_{r_2}^{r_1}\frac{h(\rho)-1}{\rho^2\sqrt{h(\rho)}}\,d\rho-\int_{r_2}^{r_1}\frac{(n-1+\lambda\rho)h_r(\rho)}{2\rho h(\rho)^{3/2}}\,d\rho\right\}\\=\ &\sqrt{h(r_1)}\left\{\frac{h_r(r_2)}{\sqrt{h(r_2)}}+ \frac{(n-1)}{2}\int_{r_2}^{r_1}\frac{h(\rho)-1}{\rho^2\sqrt{h(\rho)}}\,d\rho+ \left(\frac{n-1}{r_1}+\lambda\right)\frac{1}{\sqrt{h(r_1)}}\right.\\&\qquad\left.-\left(\frac{n-1}{r_2}+\lambda\right)\frac{1}{\sqrt{h(r_2)}}+(n-1) \int_{r_2}^{r_1}\frac{d\rho}{\rho^2\sqrt{h(\rho)}}\right\}\quad\forall 0<r_2<r_1<L \end{align*} $$
$$ \begin{align*} (h^{-1/2}h_r)_r=\ &\frac{(n-1)(h-1)}{2r^2h^{1/2}}-\frac{(n-1+\lambda r)h_r}{2rh^{3/2}}\quad\forall r>0\\\Rightarrow\ h_r(r_1)=\ &\sqrt{h(r_1)}\left\{\frac{h_r(r_2)}{\sqrt{h(r_2)}}+\frac{(n-1)}{2} \int_{r_2}^{r_1}\frac{h(\rho)-1}{\rho^2\sqrt{h(\rho)}}\,d\rho-\int_{r_2}^{r_1}\frac{(n-1+\lambda\rho)h_r(\rho)}{2\rho h(\rho)^{3/2}}\,d\rho\right\}\\=\ &\sqrt{h(r_1)}\left\{\frac{h_r(r_2)}{\sqrt{h(r_2)}}+ \frac{(n-1)}{2}\int_{r_2}^{r_1}\frac{h(\rho)-1}{\rho^2\sqrt{h(\rho)}}\,d\rho+ \left(\frac{n-1}{r_1}+\lambda\right)\frac{1}{\sqrt{h(r_1)}}\right.\\&\qquad\left.-\left(\frac{n-1}{r_2}+\lambda\right)\frac{1}{\sqrt{h(r_2)}}+(n-1) \int_{r_2}^{r_1}\frac{d\rho}{\rho^2\sqrt{h(\rho)}}\right\}\quad\forall 0<r_2<r_1<L \end{align*} $$
and (3.1) follows.
We now observe that by an argument similar to the proof of Lemmas 2.3–2.6 of [Reference Hsu9] but with (1.10) and (3.1) replacing (1.6) and (2.25) of [Reference Hsu9] in the proof there, we have the following results.
Lemma 3.2 (cf. Lemmas 2.3 and 2.4 of [Reference Hsu9])
Let
![]() $2\le n\in {\mathbb Z}^+$
and
$2\le n\in {\mathbb Z}^+$
and
![]() $\lambda \in \mathbb {R}$
. Suppose
$\lambda \in \mathbb {R}$
. Suppose
![]() ${h\in C^2((0,L))}$
satisfies (1.10) in
${h\in C^2((0,L))}$
satisfies (1.10) in
![]() $(0,L)$
for some constant
$(0,L)$
for some constant
![]() $L\in (0,\infty )$
such that
$L\in (0,\infty )$
such that
![]() ${L<-(n-1)/\lambda }$
if
${L<-(n-1)/\lambda }$
if
![]() $\lambda <0$
. Then there exist constants
$\lambda <0$
. Then there exist constants
![]() $C_2>C_1>0$
such that
$C_2>C_1>0$
such that
Lemma 3.3 (cf. Lemmas 2.5 and 2.6 of [Reference Hsu9])
Let
![]() $2\le n\in {\mathbb Z}^+$
and
$2\le n\in {\mathbb Z}^+$
and
![]() $\lambda \in \mathbb {R}$
. Suppose
$\lambda \in \mathbb {R}$
. Suppose
![]() ${h\in C^2((0,L))}$
satisfies (1.10) in
${h\in C^2((0,L))}$
satisfies (1.10) in
![]() $(0,L)$
for some constant
$(0,L)$
for some constant
![]() $L\in (0,\infty )$
such that
$L\in (0,\infty )$
such that
![]() ${L<-(n-1)/\lambda }$
if
${L<-(n-1)/\lambda }$
if
![]() $\lambda <0$
. Then there exist constants
$\lambda <0$
. Then there exist constants
![]() $C_4>C_3$
such that
$C_4>C_3$
such that
We next observe that by standard ODE theory, we have the following result.
Lemma 3.4 (cf. Lemma 2.7 of [Reference Hsu9])
Let
![]() $2\le n\in {\mathbb Z}^+$
,
$2\le n\in {\mathbb Z}^+$
,
![]() $\lambda \in {\mathbb {R}}$
,
$\lambda \in {\mathbb {R}}$
,
![]() $L>0$
,
$L>0$
,
![]() $b_0\in (C_1,C_2)$
,
$b_0\in (C_1,C_2)$
,
![]() $b_1\in (C_4,C_3)$
for some constants
$b_1\in (C_4,C_3)$
for some constants
![]() $C_2>C_1>0$
, and
$C_2>C_1>0$
, and
![]() $C_3>C_4$
. Then there exists a constant
$C_3>C_4$
. Then there exists a constant
![]() $0<\delta _1<L/4$
depending only on
$0<\delta _1<L/4$
depending only on
![]() $C_1, C_2, C_3, C_4$
such that for any
$C_1, C_2, C_3, C_4$
such that for any
![]() $r_0\in (L/2,L)$
, (1.10) has a unique solution
$r_0\in (L/2,L)$
, (1.10) has a unique solution
![]() $\widetilde {h}\in C^2((r_0-\delta _1,r_0+\delta _1))$
in
$\widetilde {h}\in C^2((r_0-\delta _1,r_0+\delta _1))$
in
![]() $(r_0-\delta _1,r_0+\delta _1)$
which satisfies
$(r_0-\delta _1,r_0+\delta _1)$
which satisfies
We are now ready for the proof of Theorem 1.1.
Proof of Theorem 1.1
We will use a modification of the proof of Theorem 1.1 of [Reference Hsu9] to prove the theorem. We first observe that by Corollary 2.3, there exists a constant
![]() ${0<\varepsilon <1}$
such that (1.10) has a unique solution
${0<\varepsilon <1}$
such that (1.10) has a unique solution
![]() $h\in C^2((0,\varepsilon ])$
in
$h\in C^2((0,\varepsilon ])$
in
![]() $(0,\varepsilon ]$
which satisfies (1.11) and (2.4) with w being given by (1.12). Moreover, (2.5) holds. Let
$(0,\varepsilon ]$
which satisfies (1.11) and (2.4) with w being given by (1.12). Moreover, (2.5) holds. Let
![]() $(0,L)$
be the maximal interval of existence of solution
$(0,L)$
be the maximal interval of existence of solution
![]() $h\in C^2((0,L))$
of (1.10) in
$h\in C^2((0,L))$
of (1.10) in
![]() $(0,L)$
which satisfies (1.11). Suppose
$(0,L)$
which satisfies (1.11). Suppose
![]() $L<\infty $
. Then, by Lemmas 3.2 and 3.3, there exist constants
$L<\infty $
. Then, by Lemmas 3.2 and 3.3, there exist constants
![]() $C_2>C_1>0$
and
$C_2>C_1>0$
and
![]() $C_3>C_4$
such that (3.2) and (3.3) hold.
$C_3>C_4$
such that (3.2) and (3.3) hold.
Then, by Lemma 3.4, there exists a constant
![]() $0<\delta _1<L/4$
depending only on
$0<\delta _1<L/4$
depending only on
![]() $C_1, C_2, C_3,C_4$
such that for any
$C_1, C_2, C_3,C_4$
such that for any
![]() $r_0\in (L/2,L)$
(1.10) has a unique solution
$r_0\in (L/2,L)$
(1.10) has a unique solution
![]() $\widetilde {h}\in C^2((r_0-\delta _1,r_0+\delta _1))$
in
$\widetilde {h}\in C^2((r_0-\delta _1,r_0+\delta _1))$
in
![]() $(r_0-\delta _1,r_0+\delta _1)$
which satisfies (3.4) with
$(r_0-\delta _1,r_0+\delta _1)$
which satisfies (3.4) with
![]() $b_0=h(r_0)$
and
$b_0=h(r_0)$
and
![]() $b_1=h_r(r_0)$
. We now set
$b_1=h_r(r_0)$
. We now set
![]() $r_0=L-(\delta _1/2)$
and extend h to a function on
$r_0=L-(\delta _1/2)$
and extend h to a function on
![]() $[0,L+(\delta _1/2))$
by setting
$[0,L+(\delta _1/2))$
by setting
![]() $h(r)=\widetilde {h}(r)$
for any
$h(r)=\widetilde {h}(r)$
for any
![]() $r\in [L,L+(\delta _1/2))$
. Then
$r\in [L,L+(\delta _1/2))$
. Then
![]() $h\in C^2((0,L+(\delta _1/2)))$
is a solution of (1.10) in
$h\in C^2((0,L+(\delta _1/2)))$
is a solution of (1.10) in
![]() $(0,L+\delta _1)$
which satisfies (1.11) and (2.4). This contradicts the choice of L. Hence,
$(0,L+\delta _1)$
which satisfies (1.11) and (2.4). This contradicts the choice of L. Hence,
![]() $L=\infty $
and there exists a solution
$L=\infty $
and there exists a solution
![]() $h\in C^2((0,\infty ))$
of (1.10) which satisfies (1.11) and (2.4).
$h\in C^2((0,\infty ))$
of (1.10) which satisfies (1.11) and (2.4).
Suppose
![]() $h_1\in C^2((0,\infty ))$
is another solution of (1.10) which satisfies (1.11) and (2.4) with w being replaced by
$h_1\in C^2((0,\infty ))$
is another solution of (1.10) which satisfies (1.11) and (2.4) with w being replaced by
![]() $w_1=r^{\alpha }h_1(r)$
. Then both w and
$w_1=r^{\alpha }h_1(r)$
. Then both w and
![]() $w_1$
satisfy (2.3). Hence, both w and
$w_1$
satisfy (2.3). Hence, both w and
![]() $w_1$
satisfy (2.1) and (2.2) in
$w_1$
satisfy (2.1) and (2.2) in
![]() $(0,\varepsilon ]$
. Therefore, by Proposition 2.1,
$(0,\varepsilon ]$
. Therefore, by Proposition 2.1,
![]() $w(r)\equiv w_1(r)$
in
$w(r)\equiv w_1(r)$
in
![]() $(0,\varepsilon ]$
. Hence,
$(0,\varepsilon ]$
. Hence,
![]() $h(r)=h_1(r)$
in
$h(r)=h_1(r)$
in
![]() $(0,\varepsilon ]$
. Then, by standard ODE theory,
$(0,\varepsilon ]$
. Then, by standard ODE theory,
![]() $h(r)=h_1(r)$
in
$h(r)=h_1(r)$
in
![]() $[\varepsilon ,\infty )$
. Thus,
$[\varepsilon ,\infty )$
. Thus,
![]() $h(r)=h_1(r)$
in
$h(r)=h_1(r)$
in
![]() $(0,\infty )$
and the solution h is unique.
$(0,\infty )$
and the solution h is unique.
Proof of Theorem 1.2
By Corollary 2.4 and an argument similar to the proof of Theorem 1.1, there exists a unique solution
![]() $h\in C^2((0,\infty ))$
of (1.10) in
$h\in C^2((0,\infty ))$
of (1.10) in
![]() $(0,\infty )$
which satisfies (1.11) and (2.27) in
$(0,\infty )$
which satisfies (1.11) and (2.27) in
![]() $(0,\varepsilon )$
with w given by (1.12) for some
$(0,\varepsilon )$
with w given by (1.12) for some
![]() $0<\varepsilon <1$
. By (2.27) and the same argument as the proof of Proposition 2.5, we get (1.18) and (1.19). Suppose
$0<\varepsilon <1$
. By (2.27) and the same argument as the proof of Proposition 2.5, we get (1.18) and (1.19). Suppose
![]() $h_1\in C^2((0,\infty ))$
is another solution of (1.10) in
$h_1\in C^2((0,\infty ))$
is another solution of (1.10) in
![]() $(0,\infty )$
which satisfies (1.11) and (1.18). Then, by an argument similar to the proof of Proposition 2.5,
$(0,\infty )$
which satisfies (1.11) and (1.18). Then, by an argument similar to the proof of Proposition 2.5,
![]() $h_1(r)\equiv h(r)$
in
$h_1(r)\equiv h(r)$
in
![]() $(0,\varepsilon ]$
. Hence, by standard ODE uniqueness theory,
$(0,\varepsilon ]$
. Hence, by standard ODE uniqueness theory,
![]() $h_1(r)\equiv h(r)$
in
$h_1(r)\equiv h(r)$
in
![]() $[\varepsilon ,\infty )$
and the theorem follows.
$[\varepsilon ,\infty )$
and the theorem follows.
Finally, by Theorem 1.1 and an argument similar to the proof of Proposition 2.6, we get Theorem 1.3.
Proof of Theorem 1.4
Without loss of generality, we may assume that
![]() $\varepsilon =2$
. Let w be given by (1.12) and
$\varepsilon =2$
. Let w be given by (1.12) and
We first claim that there exists a decreasing sequence
![]() $\{r_i\}_{i=1}^{\infty }\subset (0,\varepsilon )$
such that
$\{r_i\}_{i=1}^{\infty }\subset (0,\varepsilon )$
such that
To prove the claim, we note that by (1.12),
For any
![]() $i\in {\mathbb Z}^+$
by the mean value theorem, there exists
$i\in {\mathbb Z}^+$
by the mean value theorem, there exists
![]() $r_i\in (1/(2i),1/i)$
such that
$r_i\in (1/(2i),1/i)$
such that
 $$ \begin{align*} &|\alpha+q(r_i)|\le\frac{2ir_i|w(1/i)-w(1/(2i))|}{w(r_i)}\le\frac{2|w(1/i)-w(1/(2i))|}{w(r_i)}\quad\forall i\in{\mathbb Z}^+\\ \Rightarrow\quad&\lim_{i\to\infty}|\alpha+q(r_i)|=0 \end{align*} $$
$$ \begin{align*} &|\alpha+q(r_i)|\le\frac{2ir_i|w(1/i)-w(1/(2i))|}{w(r_i)}\le\frac{2|w(1/i)-w(1/(2i))|}{w(r_i)}\quad\forall i\in{\mathbb Z}^+\\ \Rightarrow\quad&\lim_{i\to\infty}|\alpha+q(r_i)|=0 \end{align*} $$
and the claim follows. By (1.10) and a direct computation, q satisfies
 $$ \begin{align} q_r(r)+\left(-\frac{1}{r}+\frac{\lambda}{2h(r)}+\frac{n-1}{2rh(r)}\right)q(r)=-\frac{1}{2r}\left(q(r)^2-\frac{(n-1)(h(r)-1)}{h(r)}\right)\quad\forall 0<r<\varepsilon. \end{align} $$
$$ \begin{align} q_r(r)+\left(-\frac{1}{r}+\frac{\lambda}{2h(r)}+\frac{n-1}{2rh(r)}\right)q(r)=-\frac{1}{2r}\left(q(r)^2-\frac{(n-1)(h(r)-1)}{h(r)}\right)\quad\forall 0<r<\varepsilon. \end{align} $$
Let
 $$ \begin{align} F(r)=\mbox{exp}\left(\frac{\lambda}{2}\int_0^r\frac{d\rho}{h(\rho)} +\frac{n-1}{2}\int_0^r\frac{ d\rho}{\rho h(\rho)}\right)\quad\forall 0<r<\varepsilon. \end{align} $$
$$ \begin{align} F(r)=\mbox{exp}\left(\frac{\lambda}{2}\int_0^r\frac{d\rho}{h(\rho)} +\frac{n-1}{2}\int_0^r\frac{ d\rho}{\rho h(\rho)}\right)\quad\forall 0<r<\varepsilon. \end{align} $$
Then, by (3.9),
 $$ \begin{align} &(r^{-1}F(r)q(r))_r=-\frac{F(r)}{2r^2}\left(q(r)^2-\frac{(n-1)(h(r)-1)}{h(r)}\right)\quad\forall 0<r<\varepsilon\notag\notag\\ \Rightarrow\quad&q(r)=\frac{1}{r^{-1}F(r)}(F(1)q(1)+I_1(r))\quad\forall 0<r<\varepsilon, \end{align} $$
$$ \begin{align} &(r^{-1}F(r)q(r))_r=-\frac{F(r)}{2r^2}\left(q(r)^2-\frac{(n-1)(h(r)-1)}{h(r)}\right)\quad\forall 0<r<\varepsilon\notag\notag\\ \Rightarrow\quad&q(r)=\frac{1}{r^{-1}F(r)}(F(1)q(1)+I_1(r))\quad\forall 0<r<\varepsilon, \end{align} $$
where
 $$ \begin{align} I_1(r)=\int_r^1\frac{F(\rho)}{2\rho^2}\left(q(\rho)^2-\frac{(n-1)(h(\rho)-1)}{h(\rho)}\right)\,d\rho\quad\forall 0<r<\varepsilon. \end{align} $$
$$ \begin{align} I_1(r)=\int_r^1\frac{F(\rho)}{2\rho^2}\left(q(\rho)^2-\frac{(n-1)(h(\rho)-1)}{h(\rho)}\right)\,d\rho\quad\forall 0<r<\varepsilon. \end{align} $$
We now divide the proof into two cases.
![]() $\textbf {Case 1}$
:
$\textbf {Case 1}$
:
![]() $\underset {\substack {i\to \infty }}{\limsup }|I_1(r_i)|<\infty $
.
$\underset {\substack {i\to \infty }}{\limsup }|I_1(r_i)|<\infty $
.
which contradicts the assumption that
![]() $\alpha>0$
. Hence, Case 1 does not hold.
$\alpha>0$
. Hence, Case 1 does not hold.
![]() $\textbf {Case 2}$
:
$\textbf {Case 2}$
:
![]() $\underset {\substack {i\to \infty }}{\limsup }|I_1(r_i)|=\infty $
.
$\underset {\substack {i\to \infty }}{\limsup }|I_1(r_i)|=\infty $
.
Then, we may assume, without loss of generality, that
![]() $\lim _{i\to \infty }|I_1(r_i)|=\infty $
. Since
$\lim _{i\to \infty }|I_1(r_i)|=\infty $
. Since
![]() $\alpha>0$
, by (1.11), (3.6), (3.11), and the l’Hospital rule,
$\alpha>0$
, by (1.11), (3.6), (3.11), and the l’Hospital rule,
 $$ \begin{align*} &-\alpha=\lim_{i\to\infty}q(r_i)=\lim_{i\to\infty}\frac{-\frac{F(r_i)}{2r_i^2}\left(q(r_i)^2-\frac{(n-1)(h(r_i)-1)}{h(r_i)}\right)}{-r_i^{-2}F(r_i)+r_i^{-1}F(r_i)\left(\frac{\lambda}{2 h(r_i)}+\frac{n-1}{2r_i h(r_i)} \right)}=\frac{\alpha^2-(n-1)}{2}\notag\\ \Rightarrow\quad&\alpha^2+2\alpha-(n-1)=0\notag\\ \Rightarrow\quad&\alpha=\sqrt{n}-1 \end{align*} $$
$$ \begin{align*} &-\alpha=\lim_{i\to\infty}q(r_i)=\lim_{i\to\infty}\frac{-\frac{F(r_i)}{2r_i^2}\left(q(r_i)^2-\frac{(n-1)(h(r_i)-1)}{h(r_i)}\right)}{-r_i^{-2}F(r_i)+r_i^{-1}F(r_i)\left(\frac{\lambda}{2 h(r_i)}+\frac{n-1}{2r_i h(r_i)} \right)}=\frac{\alpha^2-(n-1)}{2}\notag\\ \Rightarrow\quad&\alpha^2+2\alpha-(n-1)=0\notag\\ \Rightarrow\quad&\alpha=\sqrt{n}-1 \end{align*} $$
and the theorem follows.
4 Asymptotic behavior of the function
 $a(t)$
near the origin
$a(t)$
near the origin
In this section, we will prove the asymptotic behavior of
![]() $a(t)$
near the origin.
$a(t)$
near the origin.
Proposition Let
![]() $2\le n\in {\mathbb Z}^+$
,
$2\le n\in {\mathbb Z}^+$
,
![]() $\alpha =\sqrt {n}-1$
,
$\alpha =\sqrt {n}-1$
,
![]() $\lambda \ge 0, c_1\in {\mathbb {R}}$
,
$\lambda \ge 0, c_1\in {\mathbb {R}}$
,
![]() $c_0>0$
, and let
$c_0>0$
, and let
![]() $c_2$
be given by (1.17). For
$c_2$
be given by (1.17). For
![]() $n>4$
, let
$n>4$
, let
![]() $h\in C^2((0,\infty ))$
be the unique solution of (1.10) in
$h\in C^2((0,\infty ))$
be the unique solution of (1.10) in
![]() $(0,\infty )$
, which satisfies (1.11) and (1.18) for some constant
$(0,\infty )$
, which satisfies (1.11) and (1.18) for some constant
![]() $0<\delta _0<1$
given by Theorem 1.2. For
$0<\delta _0<1$
given by Theorem 1.2. For
![]() $n\in \{2,3,4\}$
, let
$n\in \{2,3,4\}$
, let
![]() $h\in C^2((0,\infty ))$
be given by Theorem 1.1, which satisfies (1.20) for some constant
$h\in C^2((0,\infty ))$
be given by Theorem 1.1, which satisfies (1.20) for some constant
![]() $0<\delta _0<1$
. Then
$0<\delta _0<1$
. Then
 $$ \begin{align} (h(\rho^2))^{-1/2}=&\left\{\begin{aligned} &c_0^{-1/2}\rho^{\alpha}\left(1+O(\rho^{2\alpha})\right)^{-1/2},\qquad\quad\,\mbox{if }n\ne 4\\ &c_0^{-1/2}\rho\left(1+O(\rho^4|\log\rho|^2)\right)^{-1/2},\quad\,\mbox{if }n=4 \end{aligned} \right.\notag\\ =&\left\{\begin{aligned} &c_0^{-1/2}\left(\rho^{\alpha}+O(\rho^{3\alpha})\right),\qquad\qquad\quad\kern-0.2pt\mbox{if }n\ne 4,\\ &c_0^{-1/2}\left(\rho+O(\rho^5|\log\rho|^2)\right),\quad\qquad\kern-0.2pt\mbox{if }n=4. \end{aligned} \right. \end{align} $$
$$ \begin{align} (h(\rho^2))^{-1/2}=&\left\{\begin{aligned} &c_0^{-1/2}\rho^{\alpha}\left(1+O(\rho^{2\alpha})\right)^{-1/2},\qquad\quad\,\mbox{if }n\ne 4\\ &c_0^{-1/2}\rho\left(1+O(\rho^4|\log\rho|^2)\right)^{-1/2},\quad\,\mbox{if }n=4 \end{aligned} \right.\notag\\ =&\left\{\begin{aligned} &c_0^{-1/2}\left(\rho^{\alpha}+O(\rho^{3\alpha})\right),\qquad\qquad\quad\kern-0.2pt\mbox{if }n\ne 4,\\ &c_0^{-1/2}\left(\rho+O(\rho^5|\log\rho|^2)\right),\quad\qquad\kern-0.2pt\mbox{if }n=4. \end{aligned} \right. \end{align} $$
 $$ \begin{align*} t\approx\frac{a(t)^{\sqrt{n}}}{\sqrt{nc_0}}\quad\mbox{ as }t\to 0^+ \end{align*} $$
$$ \begin{align*} t\approx\frac{a(t)^{\sqrt{n}}}{\sqrt{nc_0}}\quad\mbox{ as }t\to 0^+ \end{align*} $$
and (4.1) follows.
By a similar argument, we have the following proposition.
Proposition Let
![]() $2\le n\in {\mathbb Z}^+$
,
$2\le n\in {\mathbb Z}^+$
,
![]() $\alpha =\sqrt {n}-1$
,
$\alpha =\sqrt {n}-1$
,
![]() $\lambda , c_1\in {\mathbb {R}}$
,
$\lambda , c_1\in {\mathbb {R}}$
,
![]() $c_0>0$
, and let
$c_0>0$
, and let
![]() $c_2$
be given by (1.17). For
$c_2$
be given by (1.17). For
![]() $n>4$
, let
$n>4$
, let
![]() $h\in C^2((0,\varepsilon ])$
be the unique solution of (1.10) in
$h\in C^2((0,\varepsilon ])$
be the unique solution of (1.10) in
![]() $(0,\varepsilon ]$
, which satisfies (1.11) and (1.18) for some constants
$(0,\varepsilon ]$
, which satisfies (1.11) and (1.18) for some constants
![]() $0<\delta _0<\varepsilon <1$
, given by Proposition 2.5. For
$0<\delta _0<\varepsilon <1$
, given by Proposition 2.5. For
![]() $n\in \{2,3,4\}$
, let
$n\in \{2,3,4\}$
, let
![]() $h\in C^2((0,\varepsilon ])$
be given by Corollary 2.3, which satisfies (1.20) for some constants
$h\in C^2((0,\varepsilon ])$
be given by Corollary 2.3, which satisfies (1.20) for some constants
![]() ${0<\delta _0<\varepsilon <1}$
. Then (4.1) holds.
${0<\delta _0<\varepsilon <1}$
. Then (4.1) holds.