Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T07:47:32.922Z Has data issue: false hasContentIssue false
  • English
  • Français

Extensions of Continuous and Lipschitz Functions

Published online by Cambridge University Press:  20 November 2018

Eva Matoušková
Eva Matoušková*
Affiliation:
Mathematical Institute Czech Academy of Sciences Žitná 25 CZ-11567 Prague Czech Republic, e-mail: matouse@matsrv.math.cas.cz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show a result slightly more general than the following. Let 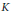$K$ be a compact Hausdorff space, 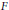$F$ a closed subset of 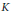$K$, and 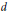$d$ a lower semi-continuous metric on 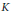$K$. Then each continuous function 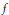$f$ on 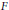$F$ which is Lipschitz in 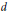$d$ admits a continuous extension on 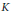$K$ which is Lipschitz in 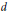$d$. The extension has the same supremum norm and the same Lipschitz constant.

As a corollary we get that a Banach space 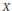$X$ is reflexive if and only if each bounded, weakly continuous and norm Lipschitz function defined on a weakly closed subset of 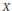$X$ admits a weakly continuous, norm Lipschitz extension defined on the entire space 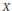$X$.

Keywords

54C2046B10extensioncontinuousLipschitzBanach space
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 2 , 01 June 2000 , pp. 208 - 217
Copyright
Copyright © Canadian Mathematical Society 2000

References

[E] Engelking, P., General Topology. PWN, Warszawa, 1977.Google Scholar
[GhMa] Ghoussoub, N. and Maurey, B., Hδ-Embedding inHilbert space and optimization on Gδ sets. Mem. Amer. Math. Soc. 62, Providence, 1986.Google Scholar
[Ja] James, R. C., Weak compactness and reflexivity. Israel Math, J.. 2(1964), 101–119.Google Scholar
[JNR] Jayne, J. E., Namioka, I. and Rogers, C. A., Norm fragmented weak* compact sets. Collect. Math. (1) 41(1990), 133–163.Google Scholar
[K] Kelley, J. L., General topology. Van, D. Nostrand Comp., New York, 1968.Google Scholar
[WW] Wells, J. H. and Williams, L. R., Embeddings and extensions in analysis. Springer-Verlag, Berlin, 1975.Google Scholar