Article contents
Extremal Values of 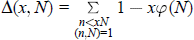
Published online by Cambridge University Press: 20 November 2018
Abstract
The function 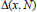 $\Delta (x,N)$ as defined in the title is closely associated via
$\Delta (x,N)$ as defined in the title is closely associated via 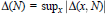 $\Delta \,(N)\,=\,{{\sup }_{x}}\,|\,\Delta (x,N)|$ to several problems in the upper bound sieve. It is also known via a classical theorem of Franel that certain conjectured bounds involving averages of
$\Delta \,(N)\,=\,{{\sup }_{x}}\,|\,\Delta (x,N)|$ to several problems in the upper bound sieve. It is also known via a classical theorem of Franel that certain conjectured bounds involving averages of 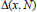 $\Delta (x,N)$ are equivalent to the Riemann Hypothesis. We improve the unconditional bounds which have been hitherto obtained for
$\Delta (x,N)$ are equivalent to the Riemann Hypothesis. We improve the unconditional bounds which have been hitherto obtained for 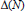 $\Delta (N)$ and show that these are close to being optimal. Several auxiliary results relating
$\Delta (N)$ and show that these are close to being optimal. Several auxiliary results relating 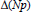 $\Delta (Np)$ to
$\Delta (Np)$ to 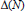 $\Delta (N)$, where
$\Delta (N)$, where  $p$ is a prime with
$p$ is a prime with 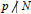 $p\nmid N$, are also obtained and two new conjectures stated.
$p\nmid N$, are also obtained and two new conjectures stated.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1998
References
- 4
- Cited by


