Article contents
Factoring a Quadratic Operator as a Product of Two Positive Contractions
Published online by Cambridge University Press: 20 November 2018
Abstract
Let  $T$ be a quadratic operator on a complex Hilbert space
$T$ be a quadratic operator on a complex Hilbert space  $H$ . We show that
$H$ . We show that  $T$ can be written as a product of two positive contractions if and only if
$T$ can be written as a product of two positive contractions if and only if  $T$ is of the form
$T$ is of the form
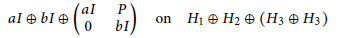 $$aI\,\oplus \,bI\,\oplus \left( \begin{matrix}aI & P\\0 & bI\\ \end{matrix} \right)\,\text{on}\,{{H}_{1}}\,\oplus \,{{H}_{2}}\,\oplus \,\left( {{H}_{3\,}}\,\oplus \,{{H}_{3}} \right)$$
$$aI\,\oplus \,bI\,\oplus \left( \begin{matrix}aI & P\\0 & bI\\ \end{matrix} \right)\,\text{on}\,{{H}_{1}}\,\oplus \,{{H}_{2}}\,\oplus \,\left( {{H}_{3\,}}\,\oplus \,{{H}_{3}} \right)$$
for some 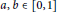 $a,\,b\,\in \,\left[ 0,\,1 \right]$ and strictly positive operator
$a,\,b\,\in \,\left[ 0,\,1 \right]$ and strictly positive operator  $P$ with
$P$ with 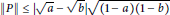 $\left\| P \right\|\,\le \,\left| \sqrt{a}-\sqrt{b} \right|\sqrt{\left( 1-a \right)\left( 1-b \right)}$ . Also, we give a necessary condition for a bounded linear operator
$\left\| P \right\|\,\le \,\left| \sqrt{a}-\sqrt{b} \right|\sqrt{\left( 1-a \right)\left( 1-b \right)}$ . Also, we give a necessary condition for a bounded linear operator  $T$ with operator matrix
$T$ with operator matrix 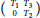 $\left( \begin{matrix} {{T}_{1}} & {{T}_{3}}\\ 0 & {{T}_{2}}\\\end{matrix} \right)$ on
$\left( \begin{matrix} {{T}_{1}} & {{T}_{3}}\\ 0 & {{T}_{2}}\\\end{matrix} \right)$ on 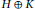 $H\,\oplus \,K$ that can be written as a product of two positive contractions.
$H\,\oplus \,K$ that can be written as a product of two positive contractions.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2016
References
- 1
- Cited by

