Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T21:58:06.131Z Has data issue: false hasContentIssue false
  • English
  • Français

A Factorization Theorem for Multiplier Algebras of Reproducing Kernel Hilbert Spaces

Published online by Cambridge University Press:  20 November 2018

Bebe Prunaru
Bebe Prunaru*
Affiliation:
Institute of Mathematics “Simion Stoilow” of the Romanian Academy, RO-014700 Bucharest, Romania e-mail: Bebe.Prunaru@imar.ro
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 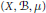$\left( X,\,B,\,\mu \right)$ be a $\sigma $-finite measure space and let 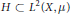$H\,\subset \,{{L}^{2}}\left( X,\,\mu \right)$ be a separable reproducing kernel Hilbert space on 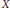$X$. We show that the multiplier algebra of 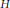$H$ has property 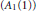$\left( {{A}_{1}}\left( 1 \right) \right)$.

Keywords

46E2247B3247L45reproducing kernel Hilbert spaceBerezin transformdual algebra
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 2 , 01 June 2013 , pp. 400 - 406
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Agler, J. and McCarthy, J. E., Pick Interpolation and Hilbert Function Spaces. Graduate Studies in Mathematics 44. American Mathematical Society, Providence RI, 2002.Google Scholar
[2] Apostol, C., Bercovici, H., C. Foias, and Pearcy, C., Invariant subspaces, dilation theory, and the structure of the predual of a dual algebra. I. J. Funct. Anal. 63(1985), no. 3, 369–404. http://dx.doi.org/10.1016/0022-1236(85)90093-X Google Scholar
[3] Aronszajn, N., Theory of reproducing kernels. Trans. Amer. Math. Soc. 68(1950), 337–404. http://dx.doi.org/10.1090/S0002-9947-1950-0051437-7 Google Scholar
[4] Beltită, D. and Prunaru, B., Amenability, completely bounded projections, dynamical systems and smooth orbits. Integral Equations Operator Theory 57(2007), no. 1, 1–17. http://dx.doi.org/10.1007/s00020-006-1446-0 Google Scholar
[5] Bercovici, H., The algebra of multiplication operators on Bergman spaces. Arch. Math. (Basel), 48(1987), no. 2, 165–174. Google Scholar
[6] Bercovici, H., Factorization theorems for integrable functions. In: Analysis at Urbana, Vol. II. London Math. Soc. Lecture Note Ser. 138. Cambridge Univ. Press, Cambridge, 1989, pp. 9–21. Google Scholar
[7] Bercovici, H., Foias, C., and Pearcy, C., Dual Algebras with Applications to Invariant Subspaces and Dilation Theory. CBMS Regional Conference Series in Mathematics 56. American Mathematical Society, Providence, RI, 1985.Google Scholar
[8] Bercovici, H. and Li, W. S., A near-factorization theorem for integrable functions. Integral Equations Operator Theory 17(1993), no. 3, 440–442. http://dx.doi.org/10.1007/BF01200295 Google Scholar
[9] Berezin, F., Covariant and contravariant symbols of operators. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 36(1972), 1134–1167. Google Scholar
[10] Choi, M. D. and Effros, E. G., The completely positive lifting problem for C-algebras. Ann. of Math. 104(1976), no. 3, 585–609. http://dx.doi.org/10.2307/1970968 Google Scholar
[11] Choi, M. D. and Effros, E. G., Injectivity and operator spaces. J. Functional Analysis 24(1977), no. 2, 156–209. http://dx.doi.org/10.1016/0022-1236(77)90052-0 Google Scholar
[12] Davidson, K. R. and Hamilton, R., Nevanlinna-Pick interpolation and factorization of linear functionals. Integral Equations Operator Theory 70(2011), no. 1, 125–149. http://dx.doi.org/10.1007/s00020-011-1862-7 Google Scholar
[13] Engliś, M., Functions invariant under the Berezin transform. J. Functional Analysis 121(1994), no. 1, 233–254. http://dx.doi.org/10.1006/jfan.1994.1048 Google Scholar
[14] Hadwin, D.W. and Nordgren, E. A., Subalgebras of reflexive algebras. J. Operator Theory 7(1982), no. 1, 3–23. Google Scholar
[15] Prunaru, B., Approximate factorization in generalized Hardy spaces. Integral Equations Operator Theory 61(2008), no. 1, 121–145. http://dx.doi.org/10.1007/s00020-008-1580-y Google Scholar
[16] Sakai, S., C*-Algebras amd W*-Algebras. Ergebnisse der Mathematik und ihrer Grenzgebiete 60. Springer-Verlag, New York, 1971.Google Scholar
[17] Stinespring, W. F., Positive functions on C*-algebras. Proc. Amer. Math. Soc. 6(1955), 211–216. Google Scholar
[18] Zhu, K., Operator Theory in Function Spaces. Second edition. Mathematical Surveys and Monographs 138. American Mathematical Society, Providence, RI, 2007 Google Scholar