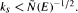Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ishihara, Hajime
and
Takahashi, Wataru
1988.
A nonlinear ergodic theorem for a reversible semigroup of Lipschitzian mappings in a Hilbert space.
Proceedings of the American Mathematical Society,
Vol. 104,
Issue. 2,
p.
431.
Kiuchi, Hirobumi
and
Takahashi, Wataru
1992.
Asymptotic behavior of almost-orbits of nonexpansive semigroups without convexity.
Kodai Mathematical Journal,
Vol. 15,
Issue. 2,
Tan, Kok-Keong
and
Xu, Hong-Kun
1993.
Fixed point theorems for Lipschitzian semigroups in Banach spaces.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 20,
Issue. 4,
p.
395.
Tan, Kok-Keong
and
Xu, Hong-Kun
1995.
Fixed points of semigroups of Lipschitzian mappings defined on nonconvex domains.
Georgian Mathematical Journal,
Vol. 2,
Issue. 5,
p.
547.
Zeng, Lu-Chuan
1995.
On the existence of fixed points and nonlinear ergodic retractions for Lipschitzian semigroups without convexity.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 24,
Issue. 9,
p.
1347.
Górnicki, Jaroslaw
1997.
Lipschitzian semigroups in Hilbert space.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 30,
Issue. 4,
p.
2309.
Lau, Anthony To-Ming
and
Takahashi, Wataru
2001.
Handbook of Metric Fixed Point Theory.
p.
517.
Marom, Saiful
and
Istiqlal, Muhammad
2023.
Fixed Point Theorems for Semigroups of Lipschitzian Mappings.
Journal of Multidisciplinary Applied Natural Science,
Vol. 4,
Issue. 1,
p.
90.

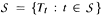 a continuous representation of
a continuous representation of 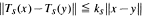 for
for 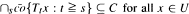 then
then 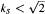 has a common fixed point in a Hilbert space. Next, we prove that the theorem is valid in a Banach space
has a common fixed point in a Hilbert space. Next, we prove that the theorem is valid in a Banach space