Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T16:35:12.431Z Has data issue: false hasContentIssue false
  • English
  • Français

Fixed Point Theorems for Proximately Nonexpansive Semigroups

Published online by Cambridge University Press:  20 November 2018

Mo Tak Kiang  and
Kok-Keong Tan
Mo Tak Kiang
Affiliation:
Department of Mathematics and Computing Science, Saint Mary's UniversityHalifax, N.S. Canada B3H 3C3
Kok-Keong Tan
Affiliation:
Department of Mathematics, Statistics And Computing Science, Dalhousie UniversityHalifax, N.S. Canada B3H 4H8
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A commutative semigroup G of continuous, selfmappings on (X, d) is called proximately nonexpansive on X if for every x in X and every (β > 0, there is a member g in G such that d(fg(x),fg(y)) ≤ (1 + β) d (x, y) for every f in G and y in X. For a uniformly convex Banach space 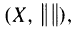it is shown that if G is a commutative semigroup of continuous selfmappings on X which is proximately nonexpansive, then a common fixed point exists if there is an x0 in X such that its orbit G(x0) is bounded. Furthermore, the asymptotic center of G(x0) is such a common fixed point.

Keywords

47H10Common fixed pointproximately nonexpansiveasymptotic center
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 29 , Issue 2 , 01 June 1986 , pp. 160 - 166
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Browder, F.E., Nonexpansive nonlinear operators in a Banach space, Proc. Nat. Acad. Sci. U.S.A., 54(1965), pp. 1041–1044.Google Scholar
2. Edelstein, M., The construction of an asymptotic center with a fixed point property, Bull. Amer. Math Soc, 78(1972), pp. 206–208.Google Scholar
3. Edelstein, M., On a fixed-point property of a reflexive, locally uniformly convex Banach space, C.R. Math Rep. Acad. Sci. Canada, 4 (1982), pp. 111–116.Google Scholar
4. Edelstein, M. and Kiang, M.T., On ultimately nonexpansive semigroups, Pac. J. of Math., 101 (1982), pp. 93–102.Google Scholar
5. Gôhde, D., Zum prinzip der kontraktiven Abbildung, Math. Nachr., 30 (1965), pp. 251–258.Google Scholar
6. Goebel, K. and Kirk, W.A., A fixed point theorem for asymptotically-nonexpansive mappings, Proc. Amer. Math Soc, 35 (1972), pp. 171–174.Google Scholar
7. Goebel, K. and Reich, S., “Uniform Convexity, Hyperbolic Geometry and Nonexpansive mappings”, Marcel Dekker, New York, 1984.Google Scholar
8. Kirk, W.A., Fixed point theory for nonexpansive mappings II, Contemporary Mathematics, Vol. 18 (1983), pp. 121–140.Google Scholar
9. Reich, S., The fixed point property for nonexpansive mappings I, II, Amer. Math. Monthly, 83 (1976), pp. 266–268. 87 (1980), pp. 292-294.Google Scholar
10. Tingley, D., An asymptotically nonexpansive commutative semigroup with no fixed points, (to appear).Google Scholar