Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-15T06:06:33.631Z Has data issue: false hasContentIssue false
  • English
  • Français

Footnote to a Formula of Gioia and Subbarao

Published online by Cambridge University Press:  20 November 2018

S. L. Segal
S. L. Segal*
Affiliation:
University of Rochester
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently Gioia and Subbarao [2] studied essentially the following problem: If g(n) is an arithmetic function, and 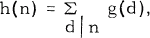, then what is the behaviour of H(a, n) defined for each fixed integer a ≥ 2 by

1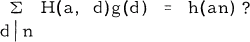

By using Vaidyanathaswamy′s formula [e.g., 1], they obtain an explicit formula for H(a, n) in case g(n) is positive and completely multiplicative (Formula 2.2 of [2]). However, Vaidyanathaswamy′s formula is unnecessary to the proof of this result, which indeed follows more simply without its use, by exploiting a simple idea used earlier by Subbarao [3] (referred to also in the course of [2]).

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 10 , Issue 5 , December 1967 , pp. 749 - 750
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. A Gioia, A., On an identity for multiplicative functions, Am. Math. Monthly 69, (1966), 988-991.Google Scholar
2. Gioia, A. A. and Subbarao, M. V., Generating functions for a class of arithmetic functions, Can. Math. Bull. 9, 1966: 427-431.Google Scholar
3. Subbarao, M. V., A generating function for a class of arithmetic functions, Am. Math. Monthly 70, (1966), 841-842.Google Scholar