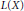Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gabriyelyan, S.
2017.
On the Ascoli property for locally convex spaces.
Topology and its Applications,
Vol. 230,
Issue. ,
p.
517.
Gabriyelyan, Saak S.
and
Morris, Sidney A.
2017.
Free topological vector spaces.
Topology and its Applications,
Vol. 223,
Issue. ,
p.
30.
Gabriyelyan, Saak
and
Ka̧kol, Jerzy
2017.
Free locally convex spaces with a small base.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 111,
Issue. 2,
p.
575.
Gabriyelyan, Saak S.
and
Morris, Sidney A.
2018.
Free Subspaces of Free Locally Convex Spaces.
Journal of Function Spaces,
Vol. 2018,
Issue. ,
p.
1.
Gabriyelyan, Saak S.
and
Morris, Sidney A.
2018.
Embedding into free topological vector spaces on compact metrizable spaces.
Topology and its Applications,
Vol. 233,
Issue. ,
p.
33.
Lin, Fucai
Lin, Shou
and
Liu, Chuan
2019.
Countable tightness and k-property of free topological vector spaces.
Topology and its Applications,
Vol. 264,
Issue. ,
p.
369.
MORRIS, SIDNEY A.
2019.
A REMARK ON THE SEPARABLE QUOTIENT PROBLEM FOR TOPOLOGICAL GROUPS.
Bulletin of the Australian Mathematical Society,
Vol. 100,
Issue. 3,
p.
453.
Lin, Fucai
and
Liu, Chuan
2020.
Notes on free topological vector spaces.
Topology and its Applications,
Vol. 281,
Issue. ,
p.
107191.
Gabriyelyan, S.
2020.
On reflexivity and the Ascoli property for free locally convex spaces.
Journal of Pure and Applied Algebra,
Vol. 224,
Issue. 11,
p.
106413.
Gabriyelyan, S.
2020.
Ascoli and sequentially Ascoli spaces.
Topology and its Applications,
Vol. 285,
Issue. ,
p.
107401.