Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-03-01T11:59:10.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Freyd's Generating Hypothesis for Groups with Periodic Cohomology

Published online by Cambridge University Press:  20 November 2018

Sunil K. Chebolu ,
J. Daniel Christensen  and
Ján Mináč
Sunil K. Chebolu
Affiliation:
Department of Mathematics, Illinois State University, Normal, IL 61761, U.S.A. e-mail: schebol@ilstu.edu
J. Daniel Christensen
Affiliation:
Department of Mathematics, University of Western Ontario, London, ON N6A 5B7 e-mail: jdc@uwo.ca minac@uwo.ca
Ján Mináč
Affiliation:
Department of Mathematics, University of Western Ontario, London, ON N6A 5B7 e-mail: jdc@uwo.ca minac@uwo.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 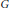$G$ be a finite group, and let $k$ be a field whose characteristic 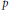$p$ divides the order of 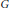$G$. Freyd's generating hypothesis for the stable module category of 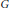$G$ is the statement that a map between finite-dimensional 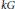$kG$-modules in the thick subcategory generated by $k$ factors through a projective if the induced map on Tate cohomology is trivial. We show that if 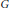$G$ has periodic cohomology, then the generating hypothesis holds if and only if the Sylow 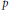$p$-subgroup of 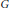$G$ is 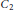${{C}_{2}}$ or 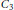${{C}_{3}}$. We also give some other conditions that are equivalent to the 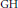$\text{GH}$ for groups with periodic cohomology.

Keywords

20C2020J0655P42Tate cohomologygenerating hypothesisstable module categoryghost mapprincipal blockthick subcategoryperiodic cohomology
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 1 , 01 March 2012 , pp. 48 - 59
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Alperin, J. L., Local representation theory. Modular representations as an introduction to the local representation theory of finite groups. Cambridge Studies in Advanced Mathematics, 11, Cambridge University Press, Cambridge, 1986.Google Scholar
[2] Benson, D. J., Cohomology of modules in the principal block of a finite group. New York J. Math. 1(1994/95), 196–205, electronic.Google Scholar
[3] Benson, D. J., Representations and cohomology. I. Basic representation theory of finite groups and associative algebras. Second ed., Cambridge Studies in Advanced Mathematics, 30, Cambridge University Press, Cambridge, 1998.Google Scholar
[4] Benson, D. J., Carlson, J. F., and Robinson, G. R., On the vanishing of group cohomology. J. Algebra 131(1990), no. 1, 40–73. doi:10.1016/0021-8693(90)90165-KGoogle Scholar
[5] Benson, D. J., Chebolu, S. K., Christensen, J. D., and Mináč, Ján, The generating hypothesis for the stable module category of a p-group. J. Algebra 310(2007), no. 1, 428–433. doi:10.1016/j.jalgebra.2006.12.013Google Scholar
[6] Carlson, J. F., Modules and group algebras. Notes by Ruedi Suter. Lectures in Mathematics ETH Zürich, Birkhäuser Verlag, Basel, 1996.Google Scholar
[7] Carlson, J. F., Chebolu, S. K., and Mináč, J., Freyd's generating hypothesis with almost split sequences. Proc. Amer. Math. Soc. 137(2009), no. 8, 2575–2580. doi:10.1090/S0002-9939-09-09826-8Google Scholar
[8] Carlson, J. F., Chebolu, S. K., and Mináč, J., Finite generation of Tate cohomology. Represent. Theory 15(2011), 244–257.Google Scholar
[9] Cartan, H. and Eilenberg, S., Homological algebra. Reprint of the 1956 original. Princeton Landmarks in Mathematics, Princeton University Press, Princeton, NJ, 1999.Google Scholar
[10] Chebolu, S. K., Christensen, J. D., and Mináč, J., Ghosts in modular representation theory. Adv. Math. 217(2008), no. 6, 2782–2799. doi:10.1016/j.aim.2007.11.008Google Scholar
[11] Chebolu, S. K., Christensen, J. D., and Mináč, J., Groups which do not admit ghosts. Proc. Amer. Math. Soc. 136(2008), no. 4, 1171–1179. doi:10.1090/S0002-9939-07-09058-2Google Scholar
[12] Curtis, C. W. and Reiner, I., Methods of representation theory. I. With applications to finite groups and orders. Reprint of the 1981 original, Wiley Classics Library, JohnWiley & Sons Inc., New York, 1990.Google Scholar
[13] Curtis, C. W. and Reiner, I., Representation theory of finite groups and associative algebras. Reprint of the 1962 original,Wiley Classics Library, John Wiley & Sons Inc., New York, 1988.Google Scholar
[14] Freyd, P., Stable homotopy. In: 1966 Proc. Conf. Categorical Algebra (La Jolla, Calif., 1965), Springer, New York, 1966, pp. 121–172.Google Scholar
[15] The GAP Group, GAP—Groups, Algorithms, and Programming, version 4.4.9, 2006. http://www.gap-system.org Google Scholar
[16] Hovey, M., Lockridge, K., and Puninski, G., The generating hypothesis in the derived category of a ring. Math. Z. 256(2007), no. 4, 789–800. doi:10.1007/s00209-007-0103-xGoogle Scholar
[17] Külshammer, B., The principal block idempotent. Arch. Math. 56(1991), no. 4, 313–319.Google Scholar
[18] Lockridge, K. H., The generating hypothesis in the derived category of R-modules. J. Pure Appl. Algebra 208(2007), no. 2, 485–495. doi:10.1016/j.jpaa.2006.01.018Google Scholar
[19] Ringel, C. M. and Tachikawa, H., QF-3 rings. J. Reine Angew. Math. 272(1974), 49–72.Google Scholar
[20] Swan, R. G., Groups with periodic cohomology. Bull. Amer. Math. Soc. 65(1959), 368–370. doi:10.1090/S0002-9904-1959-10378-5Google Scholar
[21] Webb, P. J., The Auslander-Reiten quiver of a finite group. Math. Z. 179, no. 1, 97–121. doi:10.1007/BF01173918Google Scholar
[22] Webb, P. J., Reps—a GAP package for modular representation theory, 2007. http://www.math.umn.edu/»webb/GAPfiles/ Google Scholar