From the Ideal Theorem to the class number

Abstract

In this article, we provide an explicit upper bound for 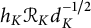$h_K \mathcal {R}_K d_K^{-1/2}$ which depends on an effective constant in the error term of the Ideal Theorem.

1 Introduction

Let K be a number field of degree $n \geqslant 3$ , signature $(r_1,r_2)$ , discriminant $(-1)^{r_2}d_K$ , class number $h_K$ , regulator $\mathcal {R}_K$ , and let $w_K$ be the number of roots of unity in K. Let $\kappa _K$ be the residue at $s=1$ of the Dedekind zeta-function $\zeta _K(s)$ attached to K. Estimating $h_K$ is a long-standing problem in algebraic number theory. One of the classic way is the use of the so-called analytic class number formula stating that

(1.1) $$ \begin{align} h_K \mathcal{R}_K = \frac{w_K }{2^n} \left( \frac{2}{\pi} \right)^{r_2} d_K^{1/2} \, \kappa_K, \end{align} $$

and to use Hecke’s integral representation and the functional equation of the Dedekind zeta-function to majorize $\kappa _K$ . This is done in [7, 8] with additional properties of log-convexity of some functions related to $\zeta _K$ which enables Louboutin to reach the following bound:

(1.2) $$ \begin{align} h_K \mathcal{R}_K \leqslant \frac{w_K}{2} \left( \frac{2}{\pi} \right)^{r_2} \left( \frac{e \log d_K}{4n-4} \right)^{n-1} d_K^{1/2}. \end{align} $$

Let $r_K(m)$ be the mth coefficient of $\zeta _K$ , i.e., the number of nonzero integral ideals of $\mathcal {O}_K$ of norm m, and denote $\Delta _K(x)$ to be the error term in the Ideal Theorem, i.e.,

(1.3) $$ \begin{align} \Delta_K(x) = \sum_{m \leqslant x} r_K(m) - \kappa_K x. \end{align} $$

The aim of this work is to prove the following result.

Theorem 1.1 Let K be an algebraic number field of degree $n \geqslant 3$ , and set $\gamma _3 = 214$ and $\gamma _n = 10$ if $n \geqslant 4$ . Assume that there exist $\alpha \in \left ( 0,\frac {2}{n} \right )$ and a constant

$$ \begin{align*} C_K \geqslant \exp \left( \max \left( \gamma_n \, , \, \alpha n + \frac{1}{4 \alpha^2}\right) \right) \end{align*} $$

such that, for $x \geqslant 1,$

(1.4) $$ \begin{align} \left | \Delta_K(x) \right | \leqslant C_K x^{1-\alpha} , \end{align} $$

where $\Delta _K(x)$ is given in (1.3). Then

$$ \begin{align*} h_K \mathcal{R}_K < \frac{3w_K}{2} \left( \frac{2}{\pi} \right)^{r_2} \left( \frac{\left( \frac{1}{2 \alpha} \log C_K \right)^{n-1}}{(n-1)!} - \frac{\left( \frac{1}{2 \alpha} \log C_K \right)^{n-2}}{(n-2)!} \right) d_K^{1/2}. \end{align*} $$

2 Tools

The first lemma is a Titchmarsh-like generalization of [12, Theorem 12.5] to number fields established by Ayoub [1]. The result is stated for the quadratic case, but as it can be seen in the proof and as the author points it out, it is still true for the general case (see also [5, Lemma 13.3]).

Lemma 2.1 Let $n \geqslant 3$ and $\mu _K$ be the infimum of the real numbers $\sigma $ for which the integral

$$ \begin{align*} \int_{- \infty}^{\infty} \frac{| \zeta_K ( \sigma + it) |^2}{| \sigma + it |^2} \, \mathrm{d}t \end{align*} $$

converges. Then $\mu _K \leqslant 1 - \frac {2}{n}$ and, for all $\mu _K < \sigma < 1$ , we have

$$ \begin{align*} \frac{1}{2 \pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( \sigma + it) |^2}{| \sigma + it |^2} \, \mathrm{d}t = \int_0^{\infty} \Delta_K(x)^2 x^{-1-2\sigma} \, \mathrm{d}x. \end{align*} $$

Proof Assume $\frac {1}{n} \leqslant \sigma \leqslant 1 - \frac {1}{n}$ . By [3, Theorem 4], we have, for all $\varepsilon> 0,$

$$ \begin{align*} \int_{1}^T | \zeta_K ( \sigma + it) |^2 \, \textrm{d}t \ll T^{n(1-\sigma) + \varepsilon}. \end{align*} $$

The exponent of T is less than $2$ for $\sigma> 1 - \frac {2-\varepsilon }{n}$ and note that $1 - \frac {2}{n} \geqslant \frac {1}{n}$ since $n \geqslant 3$ . This implies that

$$ \begin{align*} \int_{T/2}^T \frac{| \zeta_K ( \sigma + it) |^2}{| \sigma + it |^2} \, \mathrm{d}t \ll T^{- \eta} \end{align*} $$

for some $\eta = \eta (\varepsilon )>0$ . Now replacing T by $2^{-j}T$ and summing over $j \geqslant 1$ yields $\mu _K \leqslant 1 - \frac {2}{n}$ . For the second part of the lemma, we start by using Perron’s formula [11, (2.3) p. 217] yielding

$$ \begin{align*} {\sideset{^{\phantom{\prime}}}{^\prime}\sum}_{n \leqslant x} r_K(n) = \frac{1}{2 \pi i} \int_{2-i \infty}^{2+i \infty} \frac{\zeta_K(s)}{s} x^s \, \textrm{d}s, \end{align*} $$

where ${\sideset {^{\phantom {\prime }}}{^\prime }\sum }$ means that if x is a positive integer, then $\frac {1}{2} r_K(x)$ comes instead of $r_K(x)$ . Moving the line of integration to some $1- (600)^{-2/3} n^{-7/3} \leqslant c < 1$ sufficiently close to $1$ , we get

$$ \begin{align*} {\sideset{^{\phantom{\prime}}}{^\prime}\sum}_{n \leqslant x} r_K(n) = \kappa_K x + \frac{1}{2 \pi i} \int_{c-i \infty}^{c+i \infty} \frac{\zeta_K(s)}{s} x^s \, \textrm{d}s, \end{align*} $$

so that

(2.1) $$ \begin{align} \Delta_K(x) = \frac{1}{2 \pi i} \lim_{T \to \infty} \int_{c-i T}^{c+i T} \frac{\zeta_K(s)}{s} x^s \, \textrm{d}s. \end{align} $$

Using [9] (see also [2, Theorem 7.18]), there exists an absolute constant $c_0> 0$ such that, for $1- (600)^{-2/3} n^{-7/3} \leqslant c < \sigma < 1$ and $t \geqslant e,$

$$ \begin{align*} \left| \frac{\zeta_K(\sigma+it)}{\sigma+it} \right| \leqslant e^{c_0 n^8 d_K^2} \, t^{600 n^{7/2} (1-\sigma)^{3/2}-1} (\log t)^{2/3} \leqslant e^{c_0 n^8 d_K^2} \, t^{-1} (\log t)^{2/3}, \end{align*} $$

so that $\zeta _K(s) s^{-1} \to 0$ uniformly in the strip $1- (600)^{-2/3} n^{-7/3} \leqslant c < \sigma < 1$ as $|t| \to \infty $ . Hence, on integrating over the rectangle $d \pm i T$ , $c \pm iT$ , with $\gamma _K < d < c < 1$ , we infer that (2.1) holds for any $\gamma _K < c < 1$ . Replacing in (2.1) x by $1/x$ , taking $\gamma _K < c < 1$ , and using Parseval’s formula [5, Identity (A5)] yields

$$ \begin{align*} \frac{1}{2\pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( c + it) |^2}{| c + it |^2} \, \mathrm{d}t &= \int_0^{\infty} \Delta_K(1/x)^2 x^{2c-1} \, \mathrm{d}x \\ &= \int_0^{\infty} \Delta_K(u)^2 u^{-2c-1} \, \mathrm{d}u \end{align*} $$

as required.

Corollary 2.2 Assume hypothesis (1.4), and let $0 < \delta < \alpha < \frac {2}{n}$ . Then

$$ \begin{align*} \frac{1}{2 \pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( 1 - \delta + it) |}{| 1-\delta + it |^2} \, \mathrm{d}t \leqslant \frac{1}{2\sqrt{1-\delta}} \left( \frac{\kappa_K}{\sqrt{\delta}} + \frac{C_K}{\sqrt{\alpha-\delta}} \right). \end{align*} $$

Proof Using Lemma 2.1, (1.4) and the trivial bound $\left | \Delta _K(x) \right | \leqslant \kappa _K x$ when $x \in \left [ 0,1 \right )$

$$ \begin{align*} \frac{1}{2 \pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( 1 - \delta + it) |^2}{| 1-\delta + it |^2} \, \textrm{d}t & \leqslant \kappa_K^2 \int_0^1 x^{2 \delta - 1} \textrm{d}x + C_K^2 \int_1^{\infty} x^{2 (\delta-\alpha) - 1 } \textrm{d}x \\ & = \frac{1}{2} \left( \frac{\kappa_K^2}{\delta} + \frac{C_K^2}{\alpha-\delta} \right), \end{align*} $$

and using the Cauchy–Schwarz inequality, we get

$$ \begin{align*} & \frac{1}{2 \pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( 1 - \delta + it) |}{| 1-\delta + it |^2} \, \mathrm{d}t \\ & \quad \leqslant \frac{1}{2 \pi} \left( \int_{- \infty}^{\infty} \frac{| \zeta_K ( 1 - \delta + it) |^2}{| 1-\delta + it |^2} \, \textrm{d}t \right)^{1/2} \left( \int_{- \infty}^{\infty} \frac{\textrm{d}t}{ |1-\delta + it |^2} \right)^{1/2} \\ & \quad \leqslant \frac{1}{2 \sqrt{1 - \delta}} \left( \frac{\kappa_K^2}{\delta} + \frac{C_K^2}{\alpha - \delta} \right)^{1/2} \leqslant \frac{1}{2\sqrt{1-\delta}} \left( \frac{\kappa_K}{\sqrt{\delta}} + \frac{C_K}{\sqrt{\alpha-\delta}} \right) \end{align*} $$

as asserted.

Lemma 2.3 Uniformly for all $x \geqslant 1$ and all $n \in {\mathbb {Z}}_{\geqslant 1}$ , we have

$$ \begin{align*} \sum_{m \leqslant x} r_K (m) \log \frac{x}{m} \leqslant \frac{x \log x}{(n-1)!} \left( \log x+ n -1\right)^{n-2}. \end{align*} $$

Proof Let $\tau _n$ be the nth Piltz–Dirichlet divisor function. We have $r_K (m) \leqslant \tau _n(m)$ and from the bound [2, Exercise 78]

$$ \begin{align*} \sum_{m \leqslant t} \tau_n(m) \leqslant t \sum_{j=0}^{n-1} \binom{n-1}{j} \frac{(\log t)^j}{j!} \quad \left( t \geqslant 1 \right), \end{align*} $$

so that

$$ \begin{align*} \sum_{m \leqslant x} r_K (m) \log \frac{x}{m} & = \int_1^x \frac{1}{t} \left( \sum_{m \leqslant t} r_K(m) \right) \, \textrm{d}t \\ & \leqslant \sum_{j=0}^{n-1} \binom{n-1}{j} \frac{1}{j!} \int_1^x (\log t)^j \, \textrm{d}t \\ &= x \sum_{j=0}^{n-1} \binom{n-1}{j} (-1)^j \left\lbrace \sum_{k=0}^j \frac{(- \log x)^k}{k!} - \frac{1}{x} \right\rbrace \\ &= - x \sum_{j=0}^{n-1} \binom{n-1}{j} (-1)^j \sum_{k=j+1}^{\infty} \frac{(- \log x)^k}{k!} \\ &= - x \sum_{k=1}^{\infty} \frac{(- \log x)^k}{k!} \ \sum_{j=0}^{\min(n-1,k-1)} (-1)^j \binom{n-1}{j} \\ &= -x \sum_{k=1}^{\infty} (-1)^{k+\min(n-1,k-1)}\frac{(\log x)^k}{k!} \binom{n-2}{\min(n-1,k-1)} \\ &= x \sum_{k=1}^{n-1} \frac{(\log x)^k}{k!} \binom{n-2}{k-1} \\ & \leqslant \frac{x \log x}{(n-1)!} \left( \log x+ n -1\right)^{n-2}, \end{align*} $$

where we used [4, Identity (1.5)] in the $6$ th line, and the fact that, for $0 \leqslant k \leqslant n-3$ ,

$$ \begin{align*} \frac{1}{(k+1)!} &= \frac{1}{(n-1)!} \prod_{i=2}^{n-k-1} (i+k) \\ & \leqslant \frac{1}{(n-1)!} \left( \frac{1}{n-k-2} \sum_{i=2}^{n-k-1} (i+k) \right)^{n-k-2} \\ & \leqslant \frac{(n-1)^{n-k-2}}{(n-1)!} \end{align*} $$

by the GM–AM inequality stating that $\left ( a_1 \ldots a_N \right )^{1/N} \leqslant N^{-1} \left ( a_1 + \dotsb + a_N \right ) $ , where $a_k> 0$ , and this bound also holds when $k= n-2$ .

Lemma 2.4 If $n \geqslant 3$ , $0 < \alpha < \frac {2}{n}$ and $\log C_K \geqslant \gamma _n$ , then

$$ \begin{align*} \frac{\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \geqslant \frac{e^{\alpha(n-1)+1} \sqrt{\log C_K}}{\sqrt{\alpha(1-\alpha)}}. \end{align*} $$

Proof Squaring the inequality of the lemma, it is equivalent to show

$$ \begin{align*} (\log C_K)^{2n-5} \geqslant ((n-2)!)^2 \times \frac{\alpha^{2n-5} e^{2\alpha(n-1)+2}}{1-\alpha}. \end{align*} $$

The function $\alpha \in \left ( 0, \frac {2}{n} \right ) \mapsto \frac {\alpha ^{2n-5} e^{2\alpha (n-1)+2}}{1-\alpha }$ is nondecreasing, so that

$$ \begin{align*} \frac{\alpha^{2n-5} e^{2\alpha(n-1)+2}}{1-\alpha} \leqslant \frac{2^{2n-5}e^{6-4/n}n^{6-2n}}{n-2} \end{align*} $$

and, therefore, it suffices to show

$$ \begin{align*} \log C_K \geqslant 2 \left( \frac{e^{6-4/n}n^{6-2n}}{n-2} \right)^{\frac{1}{2n-5}} ((n-2)!)^{\frac{2}{2n-5}}. \end{align*} $$

Using Stirling’s bound, the inequality of the lemma is guaranteed as soon as

$$ \begin{align*} \log C_K \geqslant 2 (2 \pi)^{\frac{1}{2n-5}} e^{- \frac{12n^3-84n^2+143n-48}{6n(n-2)(2n-5)}} \left( \frac{(n-2)^{2n-4}}{n^{2n-6}}\right)^{\frac{1}{2n-5}}, \end{align*} $$

and since the right-hand side is a nonincreasing function in $n \geqslant 3$ , it then suffices that $\log C_K \geqslant s_n$ , where and whenever $n \geqslant 4$ .

3 Proof of the main result

By (1.1), it is sufficient to show that

(3.1) $$ \begin{align} \kappa_K < 3 \left( \frac{\left( \alpha^{-1} \log C_K \right)^{n-1}}{(n-1)!} - \frac{2\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \right). \end{align} $$

Assume $n \geqslant 3$ , and let $0 < \delta < \alpha < \frac {2}{n}$ and $x \geqslant 1$ satisfying

(3.2) $$ \begin{align} \delta (1-\delta) \geqslant x^{-2 \delta} \end{align} $$

and

(3.3) $$ \begin{align} x \geqslant e^{1 + \frac{1}{4 \alpha^3}}. \end{align} $$

By another Perron’s formula (see, for instance, [11, (2.9) p. 220]), we have

$$ \begin{align*}\sum_{m \leqslant x} r_K (m) \log \frac{x}{m} = \frac{1}{2 \pi i} \int_{2-i \infty}^{2+i \infty} \frac{\zeta_K(s)}{s^2} \, x^s \, \textrm{d}s.\end{align*} $$

Shifting the contour integration to the line $\sigma = 1 - \delta $ and picking up the residue of the integrand at the unique simple pole $s=1$ , we obtain by Cauchy’s theorem

$$ \begin{align*} \sum_{m \leqslant x} r_K (m) \log \frac{x}{m} & = \kappa_K x + \frac{1}{2 \pi i} \int_{1 - \delta-i \infty}^{1-\delta+i \infty} \frac{\zeta_K(s)}{s^2} \, x^s \, \textrm{d}s \\ & := \kappa_K x + I_{\delta} (x), \end{align*} $$

and using Corollary 2.2, we get

$$ \begin{align*} \left | I_{\delta} (x) \right | & \leqslant \frac{x^{1- \delta}}{2 \pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( 1 - \delta + it) |}{| 1-\delta + it |^2} \, \mathrm{d}t \\ & \leqslant \frac{x^{1-\delta}}{2\sqrt{1-\delta}} \left( \frac{\kappa_K}{\sqrt{\delta}} + \frac{C_K}{\sqrt{\alpha-\delta}} \right). \end{align*} $$

Therefore, using (3.2), we derive

$$ \begin{align*} \sum_{m \leqslant x} r_K (m) \log \frac{x}{m} & \geqslant \kappa_K x \left( 1-\frac{x^{-\delta}}{2\sqrt{\delta (1-\delta)}}\right) -\frac{x^{1-\delta}}{2} \frac{C_K}{\sqrt{(1-\delta)(\alpha-\delta)}} \\ & \geqslant \frac{\kappa_K x}{2} -\frac{x^{1-\delta}}{2} \frac{C_K}{\sqrt{(1-\delta)(\alpha-\delta)}}, \end{align*} $$

and Lemma 2.3 yields

$$ \begin{align*} \kappa_K & \leqslant \frac{2}{x} \sum_{m \leqslant x} r_K (m) \log \frac{x}{m} + \frac{x^{-\delta}C_K}{\sqrt{(1-\delta)(\alpha-\delta)}} \\ & \leqslant \frac{2 \log x}{(n-1)!} \left( \log x+ n -1\right)^{n-2} + \frac{x^{-\delta}C_K}{\sqrt{(1-\delta)(\alpha-\delta)}}, \end{align*} $$

whenever x and $\delta $ satisfy (3.2). Now choose

(3.4) $$ \begin{align} \delta = \alpha - \frac{1}{\log x}. \end{align} $$

Note that (3.2) is satisfied if $\left ( \alpha \log x - 1 \right ) \left (1 + (1-\alpha ) \log x \right ) \geqslant e^2 (\log x)^2 x^{-2\alpha }$ . But using (3.3), we get

$$ \begin{align*} \left( \alpha \log x - 1 \right) \left(1 + (1-\alpha) \log x \right) \geqslant \frac{1}{16 \alpha^2} \geqslant e^2 (\log x)^2 x^{-2\alpha}. \end{align*} $$

Therefore, with the choice (3.4), we derive

$$ \begin{align*} \kappa_K & \leqslant \frac{2 \log x}{(n-1)!} \left( \log x+ n -1\right)^{n-2} + \frac{e \, C_K x^{-\alpha} \log x}{\sqrt{(1-\alpha) \log x + 1}} \\ & < \frac{2 \log x}{(n-1)!} \left( \log x+ n -1\right)^{n-2} + \frac{e \, C_K x^{-\alpha} }{\sqrt{1-\alpha}} \sqrt{\log x} \end{align*} $$

provided that (3.3) is fulfilled. We next choose

$$ \begin{align*} x = C_K^{1/\alpha} e^{1-n}. \end{align*} $$

This yields

$$ \begin{align*} \kappa_K & < 2 \left( \frac{\left( \alpha^{-1} \log C_K \right)^{n-1}}{(n-1)!} - \frac{\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \right) + \frac{e^{\alpha(n-1)+1} \sqrt{\log C_K + \alpha(1-n)}}{\sqrt{\alpha(1-\alpha)}} \\ & < 2 \left( \frac{\left( \alpha^{-1} \log C_K \right)^{n-1}}{(n-1)!} - \frac{\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \right) + \frac{e^{\alpha(n-1)+1} \sqrt{\log C_K}}{\sqrt{\alpha(1-\alpha)}}. \end{align*} $$

Now, since $\log C_K \geqslant \gamma _n \geqslant 10> 10 - \frac {10}{n} \geqslant 5 \alpha (n-1)$ , we derive using Lemma 2.4

$$ \begin{align*} \frac{\left( \alpha^{-1} \log C_K \right)^{n-1}}{(n-1)!} - \frac{4\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} &= \frac{\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \left( \frac{\alpha^{-1}\log C_K}{n-1} - 4 \right) \\ &> \frac{\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \\ & \geqslant \frac{e^{\alpha(n-1)+1} \sqrt{\log C_K}}{\sqrt{\alpha(1-\alpha)}} \end{align*} $$

and, therefore,

$$ \begin{align*} \kappa_K < 3 \left( \frac{\left( \alpha^{-1} \log C_K \right)^{n-1}}{(n-1)!} - \frac{2\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \right) \end{align*} $$

which is (3.1). Now substituting this bound into (1.1) yields the desired result.

4 Example

Improving a result in Sunley’s thesis [10], Lee [13] proved that, for all $x> 0,$

$$ \begin{align*} \left | \Delta_K(x) \right | \leqslant \Theta_K \, d_K^{\frac{1}{n+1}} (\log d_K)^{n-1} x^{1-\frac{2}{n+1}} \end{align*} $$

with . Hence, one can take $\alpha = \frac {2}{n+1}$ and

$$ \begin{align*} C_K := \Theta_K \, d_K^{\frac{1}{n+1}} (\log d_K)^{n-1}. \end{align*} $$

The hypothesis $\log C_K \geqslant \max \left ( \gamma _n \, , \, \alpha n + \frac {1}{4 \alpha ^2}\right )$ is easily fulfilled, and noticing that, for any $n \geqslant 3,$

$$ \begin{align*}\tfrac{1}{2} n^2 \log n < \tfrac{n+1}{4} \log \Theta_K < 3 n^2 \log n, \end{align*} $$

we infer that Theorem 1.1 yields the following result.

Corollary 4.1 Let K be an algebraic number field of degree $n \geqslant 3$ . Then

$$ \begin{align*}h_K \mathcal{R}_K < \frac{3w_K}{2} \left( \frac{2}{\pi} \right)^{r_2} \left( \frac{\left (\tfrac{1}{4} \log d_K + L_K \right )^{n-1}}{(n-1)!} - \frac{\left (\tfrac{1}{4} \log d_K + \ell_K \right )^{n-2}}{(n-2)!} \right) d_K^{1/2},\end{align*} $$

where $\left. \begin {array}{c} L_K \\ \ell _K \end {array} \right \rbrace := \tfrac {1}{4} (n^2-1) \log \log d_K + \left \lbrace \begin {array}{c} 3 n^2 \log n \\ \frac {1}{2} n^2 \log n. \end {array} \right.$

Note that Stirling’s bound yields

$$ \begin{align*} h_K \mathcal{R}_K < \frac{3w_K}{2 \sqrt{2 \pi}} \left( \frac{2}{\pi} \right)^{r_2} \left\lbrace \frac{1}{\sqrt{n-1}} \left( \frac{e \log d_K}{4n-4} + \frac{e L_K}{n-1} \right)^{n-1} \right. \\ \left. - \frac{e^{-\frac{1}{12(n-2)}}}{\sqrt{n-2}} \left( \frac{e \log d_K}{4n-8} + \frac{e \ell_K}{n-2} \right)^{n-2} \right\rbrace d_K^{1/2} \end{align*} $$

which may be more easily compared to (1.2). It finally should be pointed out that Lee slightly improved in [6] the value of $C_K$ , showing that

$$ \begin{align*} C_K := \frac{0.54 \, (3n-1) \rho_K(n)}{(n-1)^2 (\log m_K)^{n-1}} \times n^{3/2} \times n! \end{align*} $$

with $m_K = (n^2 \pi /4)^{n} (n!)^{-2}$ and, if $n> 13,$

$$ \begin{align*} \rho_K(n) := (n+1)^{n-\frac{1}{2} - \frac{1}{2n}} \left( \tfrac{5}{8} + \tfrac{\pi}{2} + \tfrac{1}{n} + \tfrac{3}{8n^2} \right)^{1/2} e^{4.13 n + \frac{0.02}{n}}. \end{align*} $$

Note that the author also gives the value of $\rho _K(n)$ in the range $2 \leqslant n \leqslant 13$ . Although an improvement over the previous value of $C_K$ , this result is somewhat irrelevant on ours, while the calculations of $L_K$ and $\ell _K$ are more tedious.