No CrossRef data available.
Article contents
Full Ideals and Ring Groups in Zn[x]
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
If we add the operation of composition to the polynomial ring R[X], where R is a commutative ring with identity, we get a tri-operational algebra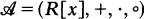 
. A full ideal or tri-operational ideal of 
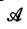is the kernel of a tri-operational homomorphism on 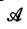. This is equivalent [4, pp. 73–74] to the following: A full ideal of 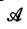is a ring ideal A of R[x] such that f°g ∈ A for every f ∈ A and g ∈ R[x].
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1976
References
1.
Carlitz, L., A Note on Permutation Functions over a Finite Field, Duke Math. Journal,
29 (1962), 325–332.Google Scholar
2.
Dickson, Leonard Eugene, Introduction to the Theory of Numbers, Dover Publications, Inc., New York, 1929.Google Scholar
3.
MacLane, Saunders and Birkhoff, Garrett, Algebra, The MacMillan Company, New York, 1967.Google Scholar
4.
Mannos, Murray, Ideals in Tri-operational Algebras I, Reports Math. Colloquium, 7 (1946), 73–79.Google Scholar
5.
Nöbauer, Wilfred, Über Gruppen von Restklassen nach Restpolynomidealen, Sitsber. Akad. Wiss. Wien, Abt. II,
162 (1953), 207–233.Google Scholar
6.
Nöbauer, Wilfred, Gruppen von Restpolynomidealrestklassen nach Primzahlpotenzen, Monatsh. f. Math.,
59 (1955), 194–202.Google Scholar
7.
Nöbauer, Wilfred, Ûber die Operation des Einsetzen in Polynomringen, Math. Ann.,
134 (1958), 248–259.Google Scholar
You have
Access