Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Smyth, Michael A.
1997.
The fixed point problem for generalised nonexpansive maps.
Bulletin of the Australian Mathematical Society,
Vol. 55,
Issue. 1,
p.
45.
Ćirić, Ljubomir B.
1999.
A new class of nonexpansive type mappings and fixed points.
Czechoslovak Mathematical Journal,
Vol. 49,
Issue. 4,
p.
891.
Dhompongsa, S.
Nanan, N.
and
Peterson, Allan C.
2011.
Fixed Point Theorems by Ways of Ultra‐Asymptotic Centers.
Abstract and Applied Analysis,
Vol. 2011,
Issue. 1,
Llorens Fuster, Enrique
Moreno Gálvez, Elena
and
Schechter, Martin D.
2011.
The Fixed Point Theory for Some Generalized Nonexpansive Mappings.
Abstract and Applied Analysis,
Vol. 2011,
Issue. 1,
Popescu, Ovidiu
2011.
Two generalizations of some fixed point theorems.
Computers & Mathematics with Applications,
Vol. 62,
Issue. 10,
p.
3912.
Karapınar, Erdal
Erhan, Inci M
and
Aksoy, Ümit
2014.
Weak "Equation missing" -contractions on partially ordered metric spaces and applications to boundary value problems.
Boundary Value Problems,
Vol. 2014,
Issue. 1,
Betiuk-Pilarska, A.
and
Domínguez Benavides, T.
2015.
The fixed point property for some generalized nonexpansive mappings and renormings.
Journal of Mathematical Analysis and Applications,
Vol. 429,
Issue. 2,
p.
800.
Balog, Laszlo
Berinde, Vasile
and
Păcurar, Mădălina
2016.
Approximating Fixed Points of Nonself Contractive Type Mappings in Banach Spaces Endowed with a Graph.
Analele Universitatii "Ovidius" Constanta - Seria Matematica,
Vol. 24,
Issue. 2,
p.
27.
Kawasaki, Toshiharu
2016.
New sufficient conditions for contractively widely more generalized hybrid mappings to have a fixed point.
Asian-European Journal of Mathematics,
Vol. 09,
Issue. 04,
p.
1650082.
LLORENS-FUSTER, ENRIQUE
2016.
ORBITALLY NONEXPANSIVE MAPPINGS.
Bulletin of the Australian Mathematical Society,
Vol. 93,
Issue. 3,
p.
497.
Suzuki, Tomonari
2017.
The weakest contractive conditions for Edelstein’s mappings to have a fixed point in complete metric spaces.
Journal of Fixed Point Theory and Applications,
Vol. 19,
Issue. 4,
p.
2361.
Kirk, W.A.
and
Shahzad, Naseer
2018.
Normal structure and orbital fixed point conditions.
Journal of Mathematical Analysis and Applications,
Vol. 463,
Issue. 2,
p.
461.
Górnicki, Jarosław
2018.
Various extensions of Kannan’s fixed point theorem.
Journal of Fixed Point Theory and Applications,
Vol. 20,
Issue. 1,
Amini-Harandi, A.
Fakhar, M.
and
Hajisharifi, H.R.
2018.
Approximate fixed points of α-nonexpansive mappings.
Journal of Mathematical Analysis and Applications,
Vol. 467,
Issue. 2,
p.
1168.
Ali, Faeem
Ali, Javid
and
Nieto, Juan J.
2020.
Some observations on generalized non-expansive mappings with an application.
Computational and Applied Mathematics,
Vol. 39,
Issue. 2,
Atailia, Sami
Redjel, Najeh
and
Dehici, Abdelkader
2020.
Some fixed point results for (c)-mappings in Banach spaces.
Journal of Fixed Point Theory and Applications,
Vol. 22,
Issue. 2,
Abdeljawad, Thabet
Ullah, Kifayat
Ahmad, Junaid
De La Sen, Manuel
Ulhaq, Azhar
and
Ahmad, Hijaz
2020.
Approximation of Fixed Points and Best Proximity Points of Relatively Nonexpansive Mappings.
Journal of Mathematics,
Vol. 2020,
Issue. ,
p.
1.
Dehici, Abdelkader
and
Redjel, Najeh
2020.
On the asymptotics of (c)-mapping iterations .
Journal of Fixed Point Theory and Applications,
Vol. 22,
Issue. 4,
Yeşilkaya, Seher Sultan
2021.
On interpolative Hardy-Rogers contractive of Suzuki type mappings.
Topological Algebra and its Applications,
Vol. 9,
Issue. 1,
p.
13.
Pant, Rajendra
Shukla, Rahul
and
Patel, Prashant
2021.
Metric Fixed Point Theory.
p.
309.
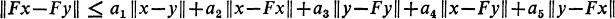
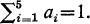 Then F has a fixed point in K.
Then F has a fixed point in K.
