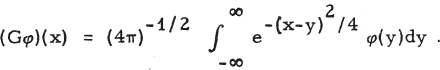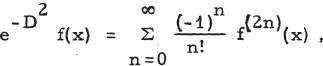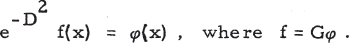Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zemanian, A. H.
1967.
A Generalized Weierstrass Transformation.
SIAM Journal on Applied Mathematics,
Vol. 15,
Issue. 4,
p.
1088.
Queen, W. C.
1971.
A Generalized Weierstrass Transformation for the Case of Several Independent Variables.
SIAM Journal on Mathematical Analysis,
Vol. 2,
Issue. 1,
p.
52.
Weinert, Ulrich
1983.
Gaussian basis functions in kinetic theory.
Physica A: Statistical Mechanics and its Applications,
Vol. 121,
Issue. 1-2,
p.
150.
Castro, L.P.
Chen, Q.
and
Saitoh, S.
2010.
Source inversion of heat conduction from a finite number of observation data.
Applicable Analysis,
Vol. 89,
Issue. 6,
p.
801.
Sookhak Lari, M.R.
and
Papini, M.
2016.
Inverse methods to gradient etch three-dimensional features with prescribed topographies using abrasive jet micro-machining: Part I – Modeling.
Precision Engineering,
Vol. 45,
Issue. ,
p.
272.
González, Benito J.
Negrín, Emilio Ramón
and
Maan, Jeetendrasingh
2024.
Abelian Theorems for the Real Weierstrass Transform over Compactly Supported Distributions.
Mathematics,
Vol. 12,
Issue. 22,
p.
3546.