Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-15T02:31:23.798Z Has data issue: false hasContentIssue false
  • English
  • Français

A Generalization of Certain Rings of A. L. Foster

Published online by Cambridge University Press:  20 November 2018

Adil Yaqub
Adil Yaqub*
Affiliation:
University of CaliforniaSanta Barbara
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The concept of a Boolean ring, as a ring A in which every element is idempotent (i. e., a2 = a for all a in A), was first introduced by Stone [4]. Boolean algebras and Boolean rings, though historically and conceptually different, were shown by Stone to be equationally interdefinable. Indeed, let (A, +, x) be a Boolean ring with unit 1, and let (A, ∪, ∩, ') be a Boolean algebra, where ∩, ∪, ', denote "union", " intersection", and "complement". The equations which convert the Boolean ring into a Boolean algebra are:

  1. I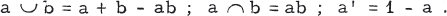

    Conversely, the equations which convert the Boolean algebra into a Boolean ring are:

  2. II

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 6 , Issue 1 , January 1963 , pp. 55 - 60
Copyright
Copyright © Canadian Mathematical Society 1963

References

1. Foster, A. L., The theory of Boolean-like rings, Trans. Amer. Math. Soc., 59(1946), 166-187.10.1090/S0002-9947-1946-0015045-5Google Scholar
2. Herstein, I. N., A generalization of a theorem of Jacobson III, Amer. J. Math., 75(1953), 105-111.10.2307/2372619Google Scholar
3. McCoy, N. H. and Montgomery, D., A representation of generalized Boolean rings, Duke Math. J., 3 (1937), 455-459.10.1215/S0012-7094-37-00335-1Google Scholar
4. Stone, M. H., The theory of representations of Boolean algebras, Trans. Amer. Math. Soc., 40 (1936), 37-111.Google Scholar
5. Yaqub, A., A note on p-like rings, Math. Magazine, 33 (1960), 287-290.10.2307/3029803Google Scholar