Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T07:23:09.878Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Equivariant Cohomology and Stratifications

Published online by Cambridge University Press:  20 November 2018

Peter Crooks  and
Tyler Holden
Peter Crooks
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON M5S 2E4 e-mail: peter.crooks@utoronto.ca tholden@math.toronto.edu e-mail: tholden@math.toronto.edu
Tyler Holden
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON M5S 2E4 e-mail: peter.crooks@utoronto.ca tholden@math.toronto.edu e-mail: tholden@math.toronto.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For 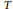$T$ a compact torus and 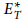$E_{T}^{*}$ a generalized 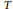$T$-equivariant cohomology theory, we provide a systematic framework for computing 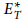$E_{T}^{*}$ in the context of equivariantly stratified smooth complex projective varieties. This allows us to explicitly compute 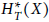$H_{T}^{*}\left( X \right)$ as an 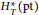$H_{T}^{*}\left( pt \right)$-module when $X$ is a direct limit of smooth complex projective 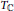${{T}_{\mathbb{C}}}$-varieties. We perform this computation on the affine Grassmannian of a complex semisimple group.

Keywords

55N9119L47equivariant cohomology theorystratificationaffine Grassmannian
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 3 , 01 September 2016 , pp. 483 - 496
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Atiyah, M. F. and Bott, R., The Yang-Mills equations over Riemann surfaces.Philos. Trans. Roy. Soc. London. Ser. A 308(1983), no. 1505, 523–615. http://dx.doi.org/10.1098/rsta.1 983.0017 Google Scholar
[2] Biatynicki-Birula, A.. Some theorems on actions of algebraic groups.Ann. of Math. 98(1973), 480–497. http://dx.doi.org/10.2307/1 97091 5 Google Scholar
[3] Cole, M., C. Greenlees, J. P., and Kriz, I., The universality of equivariant complex bordism.Math. Z. 239(2002), no. 3, 455–475. http://dx.doi.org/10.1007/s002090100315 Google Scholar
[4] Frenkel, E. and D. Ben-Zvi, Vertex algebras and algebraic curves. Second éd.,Mathematical Surveys and Monographs, 88, American Mathematical Society, Providence, RI, 2004. http://dx.doi.org/!0.1090/surv/088 Google Scholar
[5] Harada, M., Henriques, A., and Holm, T. S., Computation of generalized equivariantcohomologies ofKac-Moody flag varieties. Adv. Math. 197(2005), no. 1,198-221. http://dx.doi.org/10.101 6/j.aim.2 004.10.003 Google Scholar
[6] Hovey, M., Palmieri, J. H., and Strickland, N. P., Axiomatic stable homotopy theory.Mem.Amer. Math.Soc. 128(1997), no. 610.http://dx.doi.org/10.1090/memo/0610 Google Scholar
[7] Kamnitzer, J., Mirkovic-Vilonen cycles and polytopes. Ann. of Math.(2) 171(2010), no. 1, 245–294. http://dx.doi.org/10.4007/annals.2010.171.245 Google Scholar
[8] Kirwan, E. C., Cohomology of quotients in symplectic and algebraic geometry. Mathematical Notes, 31, Princeton University Press, Princeton, NJ, 1984.http://dx.doi.org/10.1007/BF01145470 Google Scholar
[9] Magyar, P., Schubert classes of a loop group. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.523.3671 &rep=rep1 &type=pdf Google Scholar
[10] May, J. P., Equivarianthomotopy and cohomology theory. CBMS Regional Conference Series in Mathematics, 91, Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society, Providence, RI, 1996. http://dx.doi.org/10.1090/cbms/091 Google Scholar
[11] Mirkovic, I. and Vilonen, K., Geometric Langlands duality and representations of algebraic groups over commutative rings. Ann. of Math.(2) 166(2007), no. 1, 95–143. http://dx.doi.org/10.4007/annals.2007.1 66.95 Google Scholar
[12] Mitchell, S. A., Quillen's theorem on buildings and the loops on a symmetric space. Enseign.Math. (2) 34(1988), no. 1-2, 123–166.Google Scholar
[13] Pressley, A. and Segal, G., Loop groups. Oxford Mathematical Monographs, Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 1986.Google Scholar
[14] Segal, G., Equivariant K-theory. Inst. Hautes Études Sci. Publ. Math. 34(1968), 129–151.Google Scholar
[15] Sinha, D. P., Computations of complex equivariantbordism rings. Amer. J. Math. 123(2001), no. 4, 577–605. http://dx.doi.org/10.1353/ajm.2001.0028 Google Scholar