No CrossRef data available.
Article contents
Geometric Characterizations of Hilbert Spaces
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We study some geometric properties related to the set
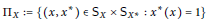 $${{\Pi }_{X}}\,:=\left\{ \left( x,\,{{x}^{*}} \right)\,\in \,{{\text{S}}_{X}}\,\times \,{{\text{S}}_{{{X}^{*}}}}\,:\,{{x}^{*}}\left( x \right)\,=\,1 \right\}$$
$${{\Pi }_{X}}\,:=\left\{ \left( x,\,{{x}^{*}} \right)\,\in \,{{\text{S}}_{X}}\,\times \,{{\text{S}}_{{{X}^{*}}}}\,:\,{{x}^{*}}\left( x \right)\,=\,1 \right\}$$
obtaining two characterizations of Hilbert spaces in the category of Banach spaces. We also compute the distance of a generic element 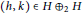 $\left( h,\,k \right)\,\in \,H\,{{\oplus }_{2}}\,H$ to
$\left( h,\,k \right)\,\in \,H\,{{\oplus }_{2}}\,H$ to 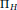 ${{\Pi }_{H}}$ for
${{\Pi }_{H}}$ for 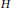 $H$ a Hilbert space.
$H$ a Hilbert space.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2016
References
[1]
Aizpuru, A. and Garcia-Pacheco, E J., L -summand vectors in Banach spaces.Vroc.
Amer. Math. Soc.
134(2006), no. 7, 2109–2115. http://dx.doi.Org/10.1090/S0002-9939-06-08243-8
Google Scholar
[2]
Chica, M., Kadets, V., Martin, M., Moreno-Pulido, S., and Rambla-Barreno, R, Bishop-Phelps-Bollobds moduli of a Banach space.
J. Math. Anal. Appl.
412(2014), 697–719. http://dx.doi.Org/10.1016/j.jmaa.2O13.10.083
Google Scholar
[3]
Deville, R., Godefroy, G., and Zizler, V., Smoothness and renormings in Banach spaces. Pitman Monographs and Surveys in Pure and Applied Mathematics 64, Longman Scientific & Technical, New York, 1993.Google Scholar
[4]
Kadets, V., Martin, M., and Paya, R., Recent progress and open questions on the numerical index of Banach spaces.
RACSAM Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Mat.
100(2006), no. 1-2, 155–182.Google Scholar


