No CrossRef data available.
Article contents
The Gibbs Phenomenon for [S, αn] Means and [T, αn ] Means
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The Gibbs phenomenon of the Fourier series 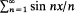 for different summability methods has been investigated by various authors. In this note, we study the same for the [S, αn ] method of summability introduced by Meir and Sharma [3]. The corresponding result for the [T, αn ] method of summability due to Powell [5] can be worked out in exactly the same way.
for different summability methods has been investigated by various authors. In this note, we study the same for the [S, αn ] method of summability introduced by Meir and Sharma [3]. The corresponding result for the [T, αn ] method of summability due to Powell [5] can be worked out in exactly the same way.
The elements c nk of the [S, αn ] matrix are defined by the relations:
1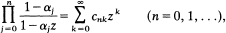
where 0<αn <1. The [S, αn ] matrix is regular if and only if 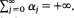
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1976
References
1.
Ishiguro, K., Zur Gibbschen Erscheinung für das Kreisverfahren. Math. Z. 76, 288-294 (1961).Google Scholar
2.
Ishiguro, K., Über das Sα-Verfahren bei Fourier-Reihen. Math. Z.
80, 4–11 (1962).10.1007/BF01162364CrossRefGoogle Scholar
3.
Meir, A. and Sharma, A., A generalization of the Sa-summation method. Proc. Camb. Phil. Soc.
67, 61–66 (1970).10.1017/S0305004100057091CrossRefGoogle Scholar
4.
Miracle, C. L., The Gibbs phenomenon for Taylor means and for [F, dn] means. Can. J. Math.
12, 660–673 (1960).10.4153/CJM-1960-059-2CrossRefGoogle Scholar
5.
Powell, R. E., The T(rn) summability transform. J. Analyse Math.
20, 289–304 (1967).10.1007/BF02786677CrossRefGoogle Scholar

