Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-13T07:06:59.587Z Has data issue: false hasContentIssue false
  • English
  • Français

Global Injectivity of C1 Maps of the Real Plane, Inseparable Leaves and the Palais–Smale Condition

Published online by Cambridge University Press:  20 November 2018

C. Gutierrez ,
X. Jarque ,
J. Llibre  and
M. A. Teixeira
C. Gutierrez
Affiliation:
Departamento de Matematica, ICMC–USP, P.O.Box 668, 13560–970 Saõ Carlos, SP, Brazil e-mail: gutp@icmc.usp.br
X. Jarque
Affiliation:
Departament de Matemàtica Aplicada i Anàlisi, Universitat de Barcelona, Gran Via, 585, 08007 Barcelona, Spain e-mail: xavier.jarque@ub.edu
J. Llibre
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Bellaterra, Barcelona, Spain e-mail: jllibre@mat.uab.es
M. A. Teixeira
Affiliation:
Departamento de Matemática, Universidade Estadual de Campinas, Caixa Postal 6065, 13083–970, Campinas, Saõ Paulo, Brazil e-mail: teixeira@ime.unicamp.br
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study two sufficient conditions that imply global injectivity for a 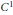${{C}^{1}}$ map 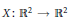$X:{{\mathbb{R}}^{2}}\to {{\mathbb{R}}^{2}}$ such that its Jacobian at any point of 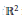${{\mathbb{R}}^{2}}$ is not zero. One is based on the notion of half-Reeb component and the other on the Palais–Smale condition. We improve the first condition using the notion of inseparable leaves. We provide a new proof of the sufficiency of the second condition. We prove that both conditions are not equivalent, more precisely we show that the Palais–Smale condition implies the nonexistence of inseparable leaves, but the converse is not true. Finally, we show that the Palais–Smale condition it is not a necessary condition for the global injectivity of the map 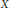$X$.

Keywords

34C3534H05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 3 , 01 September 2007 , pp. 377 - 389
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Andronov, A. A., Leontovich, E. A., Gordon, I. I., and Maier, A. L., Qualitative theory of second–order dynamic systems. Wiley, New York, 1973.Google Scholar
[2] Ambrosetti, A. and Rabinowitz, P. H., Dual variational methods in critical point theory and applications. J. Functional Analysis 14(1973), 349–381.Google Scholar
[3] Cobos, M., Gutierrez, C. and Llibre, J., On the injectivity of maps on the real plane. Canad. J. Math. 54(2001), no. 6, 1187–1201.Google Scholar
[4] van den Essen, A., Polynomial Automorphisms and the Jacobian Conjecture. Progress in Mathematics 190, Birkhauser Verlag, Basel, 2000.Google Scholar
[5] Fernandes, A., Gutierrez, C., and Rabanal, R., Global asymptotic stability for differentiable vector fields of ℝ 2 . J. Differential Equations 206(2004), no. 2, 470–482.Google Scholar
[6] Gonzales Velasco, E. A., Generic properties of polynomial vector fields at infinity. Trans. Amer. Math. Soc. 143(1969), 201–222.Google Scholar
[7] Gutierrez, C. and Nguyen, N. Ch., A remark on an eigenvalue condition for the global injectivity of differentiable maps of ℝ 2 . Disc. Cont. Dyn. Syst. 17(2007), no. 2, 397–402.Google Scholar
[8] Jarque, X. and Llibre, J., Polynomial foliations of ℝ 2 . Pacific J. Math. 197(2001), no. 1, 53–72.Google Scholar
[9] Jarque, X. and Nitecki, Z., Hamiltonian stability in the plane. Ergodic Theory Dynam. Systems 20(2000), no. 3, 775–799.Google Scholar
[10] Kaplan, W., Regular curve–families filling the plane. II. Duke Math. J. 8(1941), 11–46.Google Scholar
[11] Kotus, J., Krych, M., and Nitecki, Z., Global structural stability of flows on open surfaces. Mem. Amer. Math. Soc. 37(1982) no. 261.Google Scholar
[12] Neumann, D., Classification of continuous flows of 2-manifolds. Proc. Amer. Math. Soc. 48(1975), 73–81.Google Scholar
[13] Pinchuck, S., A counter example to the strong Jacobian conjecture. Math. Z. 217(1994), no. 1, 1–4.Google Scholar
[14] Rabinowitz, P. H., Minimax Methods in Critical Point Theory with Applications to Differential Eqautions, C.B.M.S. Regional Conference Series in Mathematics 65, American Mathematical Society, Providence, RI, 1986.Google Scholar
[15] de B. e Silva, E. A. and Teixeira, M. A., A version of Rolle's Theorem and applications. Bol. Soc. Brasil. Mat. 29(1998), no. 2, 301–328.Google Scholar
[16] de B. e Silva, E. A. and Teixeira, M. A., Global injectivity and asymptotic stability via minimax method. In: Progress in Nonlinear Analysis Nankai Ser. Pure Appl. Math. Theoret. Phys. 6, World Sci. Publishing, River Edge, NJ, 2000, pp. 339–358.Google Scholar