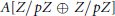Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Okon, James S.
and
Rush, David E.
2002.
GENERATING IDEALS IN COMMUTATIVE ARTINIAN GROUP RINGS AND A GENERALIZE D PASCAL'S TRIANGLE.
Communications in Algebra,
Vol. 30,
Issue. 11,
p.
5595.
Harima, Tadahito
Maeno, Toshiaki
Morita, Hideaki
Numata, Yasuhide
Wachi, Akihito
and
Watanabe, Junzo
2013.
The Lefschetz Properties.
Vol. 2080,
Issue. ,
p.
201.
Harima, Tadahito
Maeno, Toshiaki
Morita, Hideaki
Numata, Yasuhide
Wachi, Akihito
and
Watanabe, Junzo
2013.
The Lefschetz Properties.
Vol. 2080,
Issue. ,
p.
157.
Harima, Tadahito
Maeno, Toshiaki
Morita, Hideaki
Numata, Yasuhide
Wachi, Akihito
and
Watanabe, Junzo
2013.
The Lefschetz Properties.
Vol. 2080,
Issue. ,
p.
97.
Harima, Tadahito
Maeno, Toshiaki
Morita, Hideaki
Numata, Yasuhide
Wachi, Akihito
and
Watanabe, Junzo
2013.
The Lefschetz Properties.
Vol. 2080,
Issue. ,
p.
39.
Harima, Tadahito
Maeno, Toshiaki
Morita, Hideaki
Numata, Yasuhide
Wachi, Akihito
and
Watanabe, Junzo
2013.
The Lefschetz Properties.
Vol. 2080,
Issue. ,
p.
1.
Harima, Tadahito
Maeno, Toshiaki
Morita, Hideaki
Numata, Yasuhide
Wachi, Akihito
and
Watanabe, Junzo
2013.
The Lefschetz Properties.
Vol. 2080,
Issue. ,
p.
189.
Harima, Tadahito
Maeno, Toshiaki
Morita, Hideaki
Numata, Yasuhide
Wachi, Akihito
and
Watanabe, Junzo
2013.
The Lefschetz Properties.
Vol. 2080,
Issue. ,
p.
171.
Harima, Tadahito
Maeno, Toshiaki
Morita, Hideaki
Numata, Yasuhide
Wachi, Akihito
and
Watanabe, Junzo
2013.
The Lefschetz Properties.
Vol. 2080,
Issue. ,
p.
141.
Harima, Tadahito
Maeno, Toshiaki
Morita, Hideaki
Numata, Yasuhide
Wachi, Akihito
and
Watanabe, Junzo
2013.
The Lefschetz Properties.
Vol. 2080,
Issue. ,
p.
211.