Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T05:49:47.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Growth of Fine Selmer Groups in Infinite Towers

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  13 March 2020

Debanjana Kundu
Debanjana Kundu*
Affiliation:
Department of Mathematics, University of Toronto, Bahen Centre, 40 St. George St., Room 6290, Toronto, ON, M5S 2E4 Email: dkundu@math.utoronto.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the growth of fine Selmer groups in two cases. First, we study the growth of fine Selmer ranks in multiple $\mathbb{Z}_{p}$-extensions. We show that the growth of the fine Selmer group is unbounded in such towers. We recover a sufficient condition to prove the 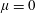$\unicode[STIX]{x1D707}=0$ conjecture for cyclotomic 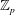$\mathbb{Z}_{p}$-extensions. We show that in certain non-cyclotomic 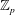$\mathbb{Z}_{p}$-towers, the 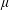$\unicode[STIX]{x1D707}$-invariant of the fine Selmer group can be arbitrarily large. Second, we show that in an unramified 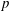$p$-class field tower, the growth of the fine Selmer group is unbounded. This tower is non-Abelian and non-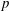$p$-adic analytic.

Keywords

Iwasawa theoryfine Selmer groupsclass groupsp-rank

MSC classification

Primary: 11R23: Iwasawa theory
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 4 , December 2020 , pp. 921 - 936
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aribam, C. S., On the 𝜇-invariant of fine Selmer groups. J. Number Theory 135(2014), 284–300. https://doi.org/10.1016/j.jnt.2013.08.003CrossRefGoogle Scholar
Bertolini, M., Iwasawa theory for elliptic curves over imaginary quadratic fields. 21st Journées Arithmétiques (Rome, 2001). J. Nombres Bordeaux 13(2001), 1–25.CrossRefGoogle Scholar
Boston, N., Some cases of the Fontaine-Mazur conjecture. J. Number Theory 42(1992), 285–291. https://doi.org/10.1016/0022-314X(92)90093-5CrossRefGoogle Scholar
Česnavičius, K., Selmer groups and class groups. Compos. Math. 151(2015), 416–434. https://doi.org/10.1112/S0010437X14007441CrossRefGoogle Scholar
Chevalley, C., Sur la théorie du corps de classes dans les corps finis et les corps locaux. Thèses de l’entre-deux-guerres 155(1934), 365–476.Google Scholar
Coates, J. and Sujatha, R., Fine Selmer groups of elliptic curves over p-adic Lie extensions. Math. Ann. 331(2005), 809–839. https://doi.org/10.1007/s00208-004-0609-zCrossRefGoogle Scholar
de Shalit, E., Iwasawa theory of elliptic curves with complex multiplication.. Perspectives in Mathematics, 3, Academic Press, Boston, MA, 1987.Google Scholar
Golod, E. S. and Shafarevich, I. R., On the class field tower. Izv. Akad. Nauk. SSSR Ser. Mat. 28(1964), 261–272. https://doi.org/10.1006/jabr.1996.6849Google Scholar
Hajir, F., On the growth of p-class groups in p-class field towers. J. Algebra 188(1997), 256–271. https://doi.org/10.1006/jabr.1996.6849CrossRefGoogle Scholar
Hajir, F. and Maire, C., Prime decomposition and the Iwasawa 𝜇-invariant. Math. Proc. Cambridge Philos. Soc. 166(2019), 599–617. https://doi.org/10.1017/S0305004118000191CrossRefGoogle Scholar
Iwasawa, K., On Z-extensions of algebraic number fields. Ann. of Math. 98(1973), 246–326. https://doi.org/10.2307/1970784CrossRefGoogle Scholar
Iwasawa, K., On the 𝜇-invariants of Z-extensions. In: Number theory, algebraic geometry and commutative algebra. Kinokuniya, Tokyo, 1973, pp. 1–11.Google Scholar
Kato, K., p-adic Hodge theory and values of zeta functions of modular forms. Astérisque 295(2004), 117–290.Google Scholar
Lemmermeyer, F., The ambiguous class number formula revisited. J. Ramanujan Math. Soc. 28(2013), 415–421.Google Scholar
Lim, M. and Sujatha, R., On the structure of fine Selmer groups and Selmer groups of CM elliptic curves. In preparation.Google Scholar
Lim, M. F. and Murty, V. K., Growth of Selmer groups of CM abelian varieties. Canad. J. Math. 67(2015), 654–666. https://doi.org/10.4153/CJM-2014-041-1CrossRefGoogle Scholar
Lim, M. F. and Murty, V. K., The growth of fine Selmer groups. J. Ramanujan Math. Soc. 31(2016), 79–94.Google Scholar
Lubotzky, A. and Mann, A., Powerful p-groups. II. p-adic analytic groups. J. Algebra 105(1987), 506–515. https://doi.org/10.1016/0021-8693(87)90212-2CrossRefGoogle Scholar
Matar, A., Selmer groups and generalized class field towers. Int. J. Number Theory 8(2012), 881–909. https://doi.org/10.1142/S1793042112500522CrossRefGoogle Scholar
Matar, A., On the 𝛬-cotorsion subgroup of the Selmer group. Asian J. Math., to appear.Google Scholar
Mazur, B., Rational points of abelian varieties with values in towers of number fields. Invent. Math. 18(1972), 183–266. https://doi.org/10.1007/BF01389815CrossRefGoogle Scholar
Monsky, P., The Hilbert-Kunz function. Math. Annalen 263(1983), 43–49. https://doi.org/10.1007/BF01457082CrossRefGoogle Scholar
Monsky, P., p-ranks of class groups in Zd p-extensions. Math. Ann. 263(1983), 509–514. https://doi.org/10.1007/BF01457057CrossRefGoogle Scholar
Murty, V. K. and Ouyang, Y., The growth of Selmer ranks of an abelian variety with complex multiplication. Pure Appl. Math. Q. 2(2006), 539–555. https://doi.org/10.4310/PAMQ.2006.v2.n2.a7CrossRefGoogle Scholar
Neukirch, J., Schmidt, A., and Wingberg, K., Cohomology of number fields. Second ed., Fundamental Principles of Mathematical Sciences, 23, Springer-Verlag, Berlin, 2008. https://doi.org/10.1007/978-3-540-37889-1CrossRefGoogle Scholar
Ozaki, M., Construction of Zp-extensions with prescribed Iwasawa modules. J. Math. Soc. Japan 56(2004), 787–801. https://doi.org/10.2969/jmsj/1191334086CrossRefGoogle Scholar
Perrin-Riou, B., Arithmétique des courbes elliptiques et théorie d’iwasawa. Mém. Soc. Math. France 17(1984), 1–130.Google Scholar
Rubin, K., Tate–Shafarevich groups of elliptic curves with complex multiplication. In: Algebraic number theory- Adv. Stud. Pure Math., 17. Academic Press, Boston, MA, 1989. https://doi.org/10.2969/aspm/01710409Google Scholar
Rubin, K., Euler systems. Annals of Mathematics Studies, 147, Princeton University Press, Princeton, NJ, 2000. https://doi.org/10.1515/9781400865208CrossRefGoogle Scholar
Serre, J.-P. and Tate, J., Good reduction of abelian varieties. Ann. of Math. 88(1968), 492–517. https://doi.org/10.2307/1970722CrossRefGoogle Scholar
Wuthrich, C., The fine Selmer group and height pairings. PhD. thesis, University of Cambridge, 2004.Google Scholar