No CrossRef data available.
Published online by Cambridge University Press: 04 January 2019
We show that Hermite’s theorem fails for every integer  $n$ of the form
$n$ of the form 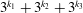 $3^{k_{1}}+3^{k_{2}}+3^{k_{3}}$ with integers
$3^{k_{1}}+3^{k_{2}}+3^{k_{3}}$ with integers 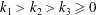 $k_{1}>k_{2}>k_{3}\geqslant 0$. This confirms a conjecture of Brassil and Reichstein. We also obtain new results for the relative Hermite–Joubert problem over a finitely generated field of characteristic 0.
$k_{1}>k_{2}>k_{3}\geqslant 0$. This confirms a conjecture of Brassil and Reichstein. We also obtain new results for the relative Hermite–Joubert problem over a finitely generated field of characteristic 0.