Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Roberts, Leslie G.
1976.
𝑆𝐾₁ of 𝑛 lines in the plane.
Transactions of the American Mathematical Society,
Vol. 222,
Issue. 0,
p.
353.
Galántai, A.
and
Hegedűs, C. J.
2008.
Perturbation bounds for polynomials.
Numerische Mathematik,
Vol. 109,
Issue. 1,
p.
77.
Guersenzvaig, N.H.
and
Szechtman, Fernando
2012.
Is every matrix similar to a polynomial in a companion matrix?.
Linear Algebra and its Applications,
Vol. 437,
Issue. 7,
p.
1611.

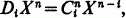 where the integer
where the integer 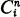 is the binomial coefficient n!;/i!;(n —i)!;. We adopt the usual convention that
is the binomial coefficient n!;/i!;(n —i)!;. We adopt the usual convention that 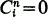 if i>9 or j<0. Then
if i>9 or j<0. Then 