Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T22:25:17.697Z Has data issue: false hasContentIssue false
  • English
  • Français

Homological Planes in the Grothendieck Ring of Varieties

Published online by Cambridge University Press:  20 November 2018

Julien Sebag
Julien Sebag*
Affiliation:
Institut de recherche mathámatique de Rennes, UMR 6625 du CNRS, Universit´e de Rennes 1, Campus de Beaulieu, 35042 Rennes cedex (France). e-mail: julien.sebag@univ-rennes1.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we identify the classes of 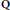$\text{Q}$-homological planes in the Grothendieck group of complex varieties 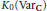${{K}_{0}}\left( \text{Va}{{\text{r}}_{\text{C}}} \right)$. Precisely, we prove that a connected, smooth, affine, complex, algebraic surface $X$ is a 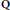$\text{Q}$-homological plane if and only if 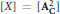$\left[ X \right]\,=\,\left[ \text{A}_{\text{C}}^{2} \right]$ in the ring 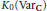${{K}_{0}}\left( \text{Va}{{\text{r}}_{\text{C}}} \right)$ and 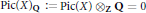$\text{Pic}{{\left( X \right)}_{\text{Q}}}\,:=\,\text{Pic}\left( X \right)\,{{\otimes }_{\text{Z}}}\,\text{Q}\,\text{=}\,\text{0}$.

Keywords

14E0514R10motivic nearby cyclesmotivic Milnor fibernearby motives
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 2 , 01 June 2015 , pp. 356 - 362
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Fujita, T., On the topology ofnoncomplete algebraic surfaces. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 29 (1982), no. 3, 503–566.Google Scholar
[2] Greenberg, M. J., Lectures on algebraic topology. W. A. Benjamin, Inc., New York-Amsterdam, 1967.Google Scholar
[3] Kraft, H., Challenging problems on affine n-space. Séminaire Bourbaki, 1994/95, Astérisque, 237 (1996), Exp. No. 802, 5, 295–317.Google Scholar
[4] Lamyand, S. Sebag, J., Birational self-maps and piecewise algebraic geometry. J. Math. Sci. Univ. Tokyo 19 (2012), no. 3, 325–357.Google Scholar
[5] Larsen, M. and Lunts, V. A., Motivic measures and stable birational geometry. Mosc. Math. J. 3 (2003), no.l, 85–95, 259.Google Scholar
[6] Liu, Q. and Sebag, J., The Grothendieck ring of varieties and piecewise isomorphisms. Math. Z. 265 (2010), no. 2, 321–342. http://dx.doi.org/10.1007/s00209-009-0518-7 Google Scholar
[7] Milnor, J., Morse theory. Annals of Mathematics Studies, 51, Princeton University Press, Princeton, NJ, 1963.Google Scholar
[8] Sebag, J., Variations on a question of Larsen and Lunts. Proc. Amer. Math. Soc. 138 (2010), no. 4, 1231–1242. http://dx.doi.org/10.1090/S0002-9939-09-10179-X Google Scholar