Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Blanc-Talon, Jacques
1998.
Advances in Pattern Recognition.
Vol. 1451,
Issue. ,
p.
140.
da Silva, A.P.
and
Sri Ranga, A.
2005.
Polynomials generated by a three term recurrence relation: bounds for complex zeros.
Linear Algebra and its Applications,
Vol. 397,
Issue. ,
p.
299.
Chen, Zhiyong
and
Iwasaki, Tetsuya
2006.
Analysis and Synthesis of Weakly Coupled Oscillators by Multivariable Harmonic Balance Approach.
p.
661.
Ales, Laurence
Carapella, Francesca
Maziero, Pricila
and
Weber, Warren E.
2008.
A model of banknote discounts.
Journal of Economic Theory,
Vol. 142,
Issue. 1,
p.
5.
Galántai, A.
and
Hegedűs, C. J.
2008.
Perturbation bounds for polynomials.
Numerische Mathematik,
Vol. 109,
Issue. 1,
p.
77.
Degla, Guy
2008.
An overview of semi-continuity results on the spectral radius and positivity.
Journal of Mathematical Analysis and Applications,
Vol. 338,
Issue. 1,
p.
101.
Chen, Zhiyong
and
Iwasaki, Tetsuya
2009.
Matrix perturbation analysis for weakly coupled oscillators.
Systems & Control Letters,
Vol. 58,
Issue. 2,
p.
148.
Galántai, Aurél
2009.
Towards Intelligent Engineering and Information Technology.
Vol. 243,
Issue. ,
p.
37.
Batra, Prashant
2010.
Globally Convergent, Iterative Path-Following for Algebraic Equations.
Mathematics in Computer Science,
Vol. 4,
Issue. 4,
p.
507.
Galántai, A.
and
Hegedüs, C.J.
2013.
Perturbations of invariant subspaces of unreduced Hessenberg matrices.
Computers & Mathematics with Applications,
Vol. 65,
Issue. 3,
p.
423.
Galántai, Aurél
2014.
Advances in Soft Computing, Intelligent Robotics and Control.
Vol. 8,
Issue. ,
p.
241.
Torrente, Maria-Laura
Beltrametti, Mauro C.
and
Sommese, Andrew J.
2017.
Perturbation results on the zero-locus of a polynomial.
Journal of Symbolic Computation,
Vol. 80,
Issue. ,
p.
307.
Bera, Sayani
Chandel, Vikramjeet Singh
and
Londhe, Mayuresh
2022.
On a Spectral Version of Cartan’s Theorem.
The Journal of Geometric Analysis,
Vol. 32,
Issue. 2,
Nafisah, Ibrahim A.
Sheikh, Sajad A.
Alshahrani, Mohammed A.
Almazah, Mohammed M. A.
Alnssyan, Badr
and
Dar, Javid Gani
2024.
Perturbation Approach to Polynomial Root Estimation and Expected Maximum Modulus of Zeros with Uniform Perturbations.
Mathematics,
Vol. 12,
Issue. 19,
p.
2993.
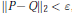 ${{\left\| P-Q \right\|}_{2}}\,<\,\varepsilon $, then the roots
${{\left\| P-Q \right\|}_{2}}\,<\,\varepsilon $, then the roots 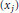 $({{x}_{j}})$ of
$({{x}_{j}})$ of  $P$ and
$P$ and 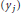 $({{y}_{j}})$ of
$({{y}_{j}})$ of 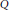 $Q$ satisfy
$Q$ satisfy 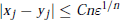 $\left| {{x}_{j}}\,-\,{{y}_{j}} \right|\,\le \,Cn{{\varepsilon }^{1/n}}$, where
$\left| {{x}_{j}}\,-\,{{y}_{j}} \right|\,\le \,Cn{{\varepsilon }^{1/n}}$, where  $n$ is the degree of
$n$ is the degree of  $P$ and
$P$ and 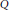 $Q$. Though there are cases where this estimate is sharp, it can still be made more precise in general, in two ways: first by using Bombieri’s norm instead of the classical
$Q$. Though there are cases where this estimate is sharp, it can still be made more precise in general, in two ways: first by using Bombieri’s norm instead of the classical 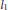 ${{l}_{1}}$ or
${{l}_{1}}$ or 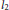 ${{l}_{2}}$ norms, and second by taking into account the multiplicity of each root. For instance, if
${{l}_{2}}$ norms, and second by taking into account the multiplicity of each root. For instance, if  $x$ is a simple root of
$x$ is a simple root of  $P$, we show that
$P$, we show that 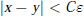 $\left| x\,-\,y \right|\,<\,C\varepsilon $ instead of
$\left| x\,-\,y \right|\,<\,C\varepsilon $ instead of 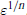 ${{\varepsilon }^{1/n}}$. The proof uses the properties of Bombieri’s scalar product andWalsh Contraction Principle.
${{\varepsilon }^{1/n}}$. The proof uses the properties of Bombieri’s scalar product andWalsh Contraction Principle.