Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cho, Hong Rae
and
Lee, Jinkee
2002.
On boundedness of the weighted Bergman projections on the Lipschitz spaces.
Bulletin of the Australian Mathematical Society,
Vol. 66,
Issue. 3,
p.
385.


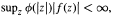 where ϕ is a positive decreasing differentiable function on [0, 1) with ϕ(1—) = 0. Concerning image area growth, criteria for
where ϕ is a positive decreasing differentiable function on [0, 1) with ϕ(1—) = 0. Concerning image area growth, criteria for 