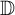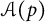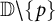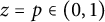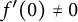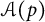1 Introduction
Let
![]() ${\mathbb D}$
be the unit disk, let
${\mathbb D}$
be the unit disk, let
![]() $\partial {\mathbb D}$
be the unit circle, and let
$\partial {\mathbb D}$
be the unit circle, and let
![]() ${\mathcal F}$
be the set of all holomorphic functions from
${\mathcal F}$
be the set of all holomorphic functions from
![]() ${\mathbb D}$
to the complex plane
${\mathbb D}$
to the complex plane
![]() ${\mathbb C}$
with
${\mathbb C}$
with
![]() $f'(0)=1$
. Given a function
$f'(0)=1$
. Given a function
![]() $f\in {\mathcal F}$
, let
$f\in {\mathcal F}$
, let
![]() $B_f$
be the radius of the largest univalent disk in
$B_f$
be the radius of the largest univalent disk in
![]() $f({\mathbb D})$
, and let
$f({\mathbb D})$
, and let
![]() $L_f$
be the radius of the largest disk in
$L_f$
be the radius of the largest disk in
![]() $f({\mathbb D})$
. Here, by a univalent disk
$f({\mathbb D})$
. Here, by a univalent disk
![]() $\Delta $
in
$\Delta $
in
![]() $f({\mathbb D})$
, we mean that there exists a domain
$f({\mathbb D})$
, we mean that there exists a domain
![]() $\Omega $
in
$\Omega $
in
![]() ${\mathbb D}$
such that f maps
${\mathbb D}$
such that f maps
![]() $\Omega $
univalently onto
$\Omega $
univalently onto
![]() $\Delta $
. In 1924, Andre Bloch—a French mathematician, proved a classical result which asserts that for
$\Delta $
. In 1924, Andre Bloch—a French mathematician, proved a classical result which asserts that for
![]() $f\in {\mathcal F}$
,
$f\in {\mathcal F}$
,
![]() $B_f>0$
(see [Reference Bloch3]). The infimum of
$B_f>0$
(see [Reference Bloch3]). The infimum of
![]() $B_f$
,
$B_f$
,
![]() $f\in {\mathcal F}$
is called the Bloch constant which we denote by B; i.e.,
$f\in {\mathcal F}$
is called the Bloch constant which we denote by B; i.e.,
This result is called as the Bloch’s theorem. In 1929, Landau (see [Reference Landau7]) first introduced the concept of Bloch constant. At the same time, he also introduced another constant, namely, the Landau constant for functions in the class
![]() ${\mathcal F}$
which is denoted by L and defined as follows:
${\mathcal F}$
which is denoted by L and defined as follows:
At present, the best known upper and lower bounds for B are
 $$ \begin{align*}\frac{\sqrt{3}}{4}+2\times 10^{-4}< B \leq \frac{1}{\sqrt{1+\sqrt{3}}}\frac{\Gamma(1/3)\Gamma(11/12)}{\Gamma(1/4)}\approx 0.4719. \end{align*} $$
$$ \begin{align*}\frac{\sqrt{3}}{4}+2\times 10^{-4}< B \leq \frac{1}{\sqrt{1+\sqrt{3}}}\frac{\Gamma(1/3)\Gamma(11/12)}{\Gamma(1/4)}\approx 0.4719. \end{align*} $$
The lower bound for the Bloch constant B was obtained by Chen and Gauthier (see [Reference Chen and Gauthier5]). The upper bound for the Bloch constant B was obtained by Ahlfors and Grunsky (see [Reference Ahlfors and Grunsky1]); also, they conjectured that this upper bound is the precise value of the Bloch constant. We now present here a brief overview of the Landau constant. In 1943, Rademacher (compare [Reference Rademacher10]) and Yanagihara (in 1995, see [Reference Yanagihara12]) proved that the upper and the lower bounds for the Landau constant are
Rademacher (compare [Reference Rademacher10]) also conjectured that this upper bound is the precise value of the Landau constant. It is worth to mention here that, after the proof of the famous Bieberbach conjecture by Louis de Branges in 1985, one of the most outstanding open problems in geometric function theory is to find the precise value of the Bloch and the Landau constants for functions in the class
![]() ${\mathcal F}$
. In the sequel, we also briefly discuss about the locally univalent and the univalent Bloch constants for holomorphic functions which are defined by
${\mathcal F}$
. In the sequel, we also briefly discuss about the locally univalent and the univalent Bloch constants for holomorphic functions which are defined by
 $$ \begin{align*} B_l&:=\inf~\{B_f:f\in{\mathcal F},\;\; f'(z)\ne 0,\; z\in{\mathbb D}\}\;\;\mbox{and}\\ B_u&:=\inf~\{B_f:f\in{\mathcal F},\;\;f\;\mbox{is univalent in}\;{\mathbb D}\}, \end{align*} $$
$$ \begin{align*} B_l&:=\inf~\{B_f:f\in{\mathcal F},\;\; f'(z)\ne 0,\; z\in{\mathbb D}\}\;\;\mbox{and}\\ B_u&:=\inf~\{B_f:f\in{\mathcal F},\;\;f\;\mbox{is univalent in}\;{\mathbb D}\}, \end{align*} $$
respectively. The relation between Bloch constant, Landau constant, locally univalent Bloch constant, and univalent Bloch constant is
In 1995, Yanagihara (see [Reference Yanagihara12]) proved that
![]() $B_l>1/2+ 10^{-335}$
. In 2009, Skinner (see [Reference Skinner11]) proved that
$B_l>1/2+ 10^{-335}$
. In 2009, Skinner (see [Reference Skinner11]) proved that
![]() $B_u>0.5708858$
. These bounds are latest bounds and best known so far.
$B_u>0.5708858$
. These bounds are latest bounds and best known so far.
Many eminent Mathematicians studied the Bloch constant for meromorphic functions considering the spherical metric, which was a natural choice for them, as meromorphic functions take values in
![]() ${\widehat {\mathbb C}}\,$
—the extended complex plane. We present here a short description of the results known so far in this direction. In [Reference Minda9], Minda proved that the precise value of the Bloch constant for the family of locally univalent meromorphic functions on
${\widehat {\mathbb C}}\,$
—the extended complex plane. We present here a short description of the results known so far in this direction. In [Reference Minda9], Minda proved that the precise value of the Bloch constant for the family of locally univalent meromorphic functions on
![]() ${\mathbb C}$
is
${\mathbb C}$
is
![]() $\pi /2$
. In the same article, he showed that the Bloch constant for the family of all nonconstant meromorphic functions on
$\pi /2$
. In the same article, he showed that the Bloch constant for the family of all nonconstant meromorphic functions on
![]() ${\mathbb C}$
lies between
${\mathbb C}$
lies between
![]() $\pi /3$
and
$\pi /3$
and
![]() $2\arctan (1/\sqrt {2})$
, which is improved by Bonk and Eremenko in the year
$2\arctan (1/\sqrt {2})$
, which is improved by Bonk and Eremenko in the year
![]() $2000$
(see [Reference Bonk and Eremenko4]) and they obtained the precise value of this constant as
$2000$
(see [Reference Bonk and Eremenko4]) and they obtained the precise value of this constant as
![]() $\arctan \sqrt {8}$
.
$\arctan \sqrt {8}$
.
In the article [Reference Bhowmik and Sen2], we considered the analogous problem of estimating the Landau and the Bloch constants for a class of meromorphic functions in the Euclidean metric. Precisely, let
![]() $\mathcal {A}(p)$
consisting of all functions f that are holomorphic in
$\mathcal {A}(p)$
consisting of all functions f that are holomorphic in
![]() ${\mathbb D}\backslash \{p\}$
with a simple pole at
${\mathbb D}\backslash \{p\}$
with a simple pole at
![]() $z=p\in (0,1)$
and
$z=p\in (0,1)$
and
![]() $f'(0)\neq 0$
. For
$f'(0)\neq 0$
. For
![]() $f\in \mathcal {A}(p)$
, let
$f\in \mathcal {A}(p)$
, let
![]() $B_f(p)$
be the radius of the largest univalent disk that lies in
$B_f(p)$
be the radius of the largest univalent disk that lies in
![]() $f({\mathbb D})$
and let
$f({\mathbb D})$
and let
![]() $L_f(p)$
be the radius of the largest disk that lies in
$L_f(p)$
be the radius of the largest disk that lies in
![]() $f({\mathbb D})$
. The Bloch and the Landau constants for
$f({\mathbb D})$
. The Bloch and the Landau constants for
![]() $f\in \mathcal {A}(p)$
are defined by
$f\in \mathcal {A}(p)$
are defined by
respectively. In [Reference Bhowmik and Sen2], we proved that
In this article, we significantly improve the lower bounds of
![]() $B(p)$
and
$B(p)$
and
![]() $L(p)$
and conjecture on the exact values of these constants.
$L(p)$
and conjecture on the exact values of these constants.
2 Main result
Theorem 2.1 If B and L be the Bloch and the Landau constants for the class
![]() ${\mathcal F}$
, then
${\mathcal F}$
, then
 $$ \begin{align*}B(p)\geq\frac{4p|f'(0)|B}{(1+p)^2}\;\;\mbox{and}\;\;L(p)\geq\frac{4p|f'(0)|L}{(1+p)^2}. \end{align*} $$
$$ \begin{align*}B(p)\geq\frac{4p|f'(0)|B}{(1+p)^2}\;\;\mbox{and}\;\;L(p)\geq\frac{4p|f'(0)|L}{(1+p)^2}. \end{align*} $$
Proof Let
![]() $\Omega _p$
be the domain obtained from the unit disk
$\Omega _p$
be the domain obtained from the unit disk
![]() ${\mathbb D}$
by deleting the line segment
${\mathbb D}$
by deleting the line segment
![]() $[p,\;1)$
, i.e.,
$[p,\;1)$
, i.e.,
Clearly,
![]() $\Omega _p$
is a simply connected domain. This domain
$\Omega _p$
is a simply connected domain. This domain
![]() $\Omega _p$
can be mapped conformally onto
$\Omega _p$
can be mapped conformally onto
![]() ${\mathbb D}$
by a function
${\mathbb D}$
by a function
![]() $\kappa $
with the following Taylor expansion in the disk
$\kappa $
with the following Taylor expansion in the disk
![]() $\{z\in {\mathbb C}~:~|z|<p\}$
about the origin
$\{z\in {\mathbb C}~:~|z|<p\}$
about the origin
 $$ \begin{align*}\kappa(z)=\frac{(1+p)^2}{4p}z + \sum_{n=2}^{\infty} c_n z^n, \end{align*} $$
$$ \begin{align*}\kappa(z)=\frac{(1+p)^2}{4p}z + \sum_{n=2}^{\infty} c_n z^n, \end{align*} $$
where
![]() $c_n>0$
for all
$c_n>0$
for all
![]() $n\geq 2$
(see, for instance, [Reference Jenkins6, Reference Löwner8]). Now, for
$n\geq 2$
(see, for instance, [Reference Jenkins6, Reference Löwner8]). Now, for
![]() $f\in {\mathcal A}(p)$
, let
$f\in {\mathcal A}(p)$
, let
![]() $f_1\equiv f|_{\Omega _p}$
. Now, for each such
$f_1\equiv f|_{\Omega _p}$
. Now, for each such
![]() $f_1$
, there exists a function
$f_1$
, there exists a function
![]() $g\in {\mathcal F}$
with g having a simple pole at
$g\in {\mathcal F}$
with g having a simple pole at
![]() $e^{i\theta }\kappa (p)\in \partial {\mathbb D}$
,
$e^{i\theta }\kappa (p)\in \partial {\mathbb D}$
,
![]() $\theta =\arg (f'(0))$
such that
$\theta =\arg (f'(0))$
such that
 $$ \begin{align*}f_1(z)=\frac{4p|f'(0)|}{(1+p)^2}(g\circ(e^{i\theta} \kappa))(z),\;z\in\Omega_p. \end{align*} $$
$$ \begin{align*}f_1(z)=\frac{4p|f'(0)|}{(1+p)^2}(g\circ(e^{i\theta} \kappa))(z),\;z\in\Omega_p. \end{align*} $$
We note here that
![]() $f_1$
is a holomorphic function in
$f_1$
is a holomorphic function in
![]() $\Omega _p$
with
$\Omega _p$
with
![]() $f_1'(0)=f'(0)$
and
$f_1'(0)=f'(0)$
and
 $$ \begin{align*}f_1(\Omega_p)=\frac{4p|f'(0)|}{(1+p)^2}g({\mathbb D}). \end{align*} $$
$$ \begin{align*}f_1(\Omega_p)=\frac{4p|f'(0)|}{(1+p)^2}g({\mathbb D}). \end{align*} $$
Since
![]() $g\in {\mathcal F}$
, then
$g\in {\mathcal F}$
, then
![]() $g({\mathbb D})$
contains a univalent disk of radius at least B and a disk of radius at least L. This implies that
$g({\mathbb D})$
contains a univalent disk of radius at least B and a disk of radius at least L. This implies that
![]() $f_1(\Omega _p)$
contains a univalent disk of radius at least
$f_1(\Omega _p)$
contains a univalent disk of radius at least
![]() $4p|f'(0)|B/(1+p)^2$
and a disk of radius at least
$4p|f'(0)|B/(1+p)^2$
and a disk of radius at least
![]() $4p|f'(0)|L/(1+p)^2$
. As
$4p|f'(0)|L/(1+p)^2$
. As
![]() $f_1(\Omega _p)\subset f({\mathbb D})$
, therefore
$f_1(\Omega _p)\subset f({\mathbb D})$
, therefore
![]() $f({\mathbb D})$
contains a univalent disk of radius at least
$f({\mathbb D})$
contains a univalent disk of radius at least
![]() $4p|f'(0)|B/(1+p)^2$
and a disk of radius at least
$4p|f'(0)|B/(1+p)^2$
and a disk of radius at least
![]() $4p|f'(0)|L/(1+p)^2$
. This completes the proof.
$4p|f'(0)|L/(1+p)^2$
. This completes the proof.
Remarks (i) Since the best known lower bound of the Bloch constant B for
![]() ${\mathcal F}$
is
${\mathcal F}$
is
![]() $\sqrt {3}/4+2\times 10^{-4}$
(compare [Reference Chen and Gauthier5]), then form Theorem 2.1, we have
$\sqrt {3}/4+2\times 10^{-4}$
(compare [Reference Chen and Gauthier5]), then form Theorem 2.1, we have
 $$ \begin{align*}B(p)>\frac{(\sqrt{3}+8\times 10^{-4})|f'(0)|p}{(1+p)^2}. \end{align*} $$
$$ \begin{align*}B(p)>\frac{(\sqrt{3}+8\times 10^{-4})|f'(0)|p}{(1+p)^2}. \end{align*} $$
This lower bound improves the lower bound proved in [Reference Bhowmik and Sen2, Theorem 2]. Also, since the best known lower bound of the Landau constant for holomorphic function is
![]() $1/2+10^{-335}$
(compare [Reference Yanagihara12]), then from the Theorem 2.1, we get
$1/2+10^{-335}$
(compare [Reference Yanagihara12]), then from the Theorem 2.1, we get
 $$ \begin{align*}L(p)>\frac{(2+4\times 10^{-335})|f'(0)|p}{(1+p)^2}. \end{align*} $$
$$ \begin{align*}L(p)>\frac{(2+4\times 10^{-335})|f'(0)|p}{(1+p)^2}. \end{align*} $$
This lower bound of the Landau constant
![]() $L(p)$
for the class of functions
$L(p)$
for the class of functions
![]() ${\mathcal A}(p)$
improves the bound given in [Reference Bhowmik and Sen2, Theorem 1].
${\mathcal A}(p)$
improves the bound given in [Reference Bhowmik and Sen2, Theorem 1].
(ii) In [Reference Bhowmik and Sen2], we have considered a subclass
![]() ${\mathcal A}_1(p)$
of
${\mathcal A}_1(p)$
of
![]() ${\mathcal A}(p)$
and improved the lower bounds of the Bloch and the Landau constants for function in
${\mathcal A}(p)$
and improved the lower bounds of the Bloch and the Landau constants for function in
![]() ${\mathcal A}_1(p)$
as
${\mathcal A}_1(p)$
as
![]() $p^2|f'(0)|/27$
and
$p^2|f'(0)|/27$
and
![]() $(9-4\sqrt {5})p^2|f'(0)|/(1+\sqrt {2})$
, respectively (see [Reference Bhowmik and Sen2, Theorems 3 and 4]). We note here that the lower bounds presented in the Remark (i) also improve the lower bounds proved in [Reference Bhowmik and Sen2, Theorems 3 and 4] for this particular subclass of
$(9-4\sqrt {5})p^2|f'(0)|/(1+\sqrt {2})$
, respectively (see [Reference Bhowmik and Sen2, Theorems 3 and 4]). We note here that the lower bounds presented in the Remark (i) also improve the lower bounds proved in [Reference Bhowmik and Sen2, Theorems 3 and 4] for this particular subclass of
![]() ${\mathcal A}(p)$
.
${\mathcal A}(p)$
.
(iii) Let
 $$ \begin{align*} &B_l(p):=\inf~\{B_f(p)\,:\,f\in{\mathcal A}(p),\;f'(z)\ne0,\;z\in{\mathbb D}\backslash\{p\}\}\;\;\mbox{and}\\ &B_u(p):=\inf~\{B_f(p)\,:\,f\in{\mathcal A}(p),\;f\;\mbox{is univalent in}\;{\mathbb D}\backslash\{p\}\}. \end{align*} $$
$$ \begin{align*} &B_l(p):=\inf~\{B_f(p)\,:\,f\in{\mathcal A}(p),\;f'(z)\ne0,\;z\in{\mathbb D}\backslash\{p\}\}\;\;\mbox{and}\\ &B_u(p):=\inf~\{B_f(p)\,:\,f\in{\mathcal A}(p),\;f\;\mbox{is univalent in}\;{\mathbb D}\backslash\{p\}\}. \end{align*} $$
Then from Theorem 2.1, we get
 $$ \begin{align*}B_l(p)>\frac{(2+4\times 10^{-335})|f'(0)|p}{(1+p)^2}\;\;\mbox{and}\;\;B_u(p)>\frac{2.2835432|f'(0)|p}{(1+p)^2}; \end{align*} $$
$$ \begin{align*}B_l(p)>\frac{(2+4\times 10^{-335})|f'(0)|p}{(1+p)^2}\;\;\mbox{and}\;\;B_u(p)>\frac{2.2835432|f'(0)|p}{(1+p)^2}; \end{align*} $$
since the lower bounds of the locally univalent and univalent Bloch constants for holomorphic functions are
![]() $1/2+ 10^{-335}$
and
$1/2+ 10^{-335}$
and
![]() $0.5708858$
, respectively.
$0.5708858$
, respectively.
(iv) We comment here that Theorem 2.1 can be generalized for functions holomorphic in
![]() ${\mathbb D}\backslash [p,1)$
,
${\mathbb D}\backslash [p,1)$
,
![]() $p\in (0,1)$
having singular points lying in the line segment
$p\in (0,1)$
having singular points lying in the line segment
![]() $[p,1)$
. The method of proof will remain the same which we adopted in the Theorem 2.1.
$[p,1)$
. The method of proof will remain the same which we adopted in the Theorem 2.1.
From Theorem 2.1, we only get information about the lower bounds of the Bloch and the Landau constants for the class
![]() ${\mathcal A}(p)$
, but we have no information about the upper bounds and the exact values of such constants. It will be an interesting problem to find upper bounds and the precise values of such constants. In Theorem 2.1, if we allow
${\mathcal A}(p)$
, but we have no information about the upper bounds and the exact values of such constants. It will be an interesting problem to find upper bounds and the precise values of such constants. In Theorem 2.1, if we allow
![]() $p\rightarrow 1-$
, then
$p\rightarrow 1-$
, then
If
![]() $f'(0)=1$
, and
$f'(0)=1$
, and
![]() $B(1)$
and
$B(1)$
and
![]() $L(1)$
denote the Bloch and the Landau constants for functions in the class
$L(1)$
denote the Bloch and the Landau constants for functions in the class
![]() ${\mathcal F}$
, with a simple pole at
${\mathcal F}$
, with a simple pole at
![]() $z=1$
, then we know that one can easily show
$z=1$
, then we know that one can easily show
![]() $B(1)=B$
and
$B(1)=B$
and
![]() $L(1)=L$
. Thus, equalities hold in the above inequalities. This observation motivates us to conjecture on the precise values of the Bloch and the Landau constants for functions in the class
$L(1)=L$
. Thus, equalities hold in the above inequalities. This observation motivates us to conjecture on the precise values of the Bloch and the Landau constants for functions in the class
![]() ${\mathcal A}(p)$
as follows:
${\mathcal A}(p)$
as follows:
Conjecture 1 If B and L are the exact values of the Bloch and the Landau constants, respectively, for functions in the class
![]() ${\mathcal F}$
, then
${\mathcal F}$
, then
 $$ \begin{align*}B(p)=\frac{4p|f'(0)|B}{(1+p)^2}~ \mbox {and}\,~ L(p)=\frac{4p|f'(0)|L}{(1+p)^2}. \end{align*} $$
$$ \begin{align*}B(p)=\frac{4p|f'(0)|B}{(1+p)^2}~ \mbox {and}\,~ L(p)=\frac{4p|f'(0)|L}{(1+p)^2}. \end{align*} $$