Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-15T06:55:24.420Z Has data issue: false hasContentIssue false
  • English
  • Français

Inadmissibility of the Maximum Likelihood Estimator in the Presence of Prior Information

Published online by Cambridge University Press:  20 November 2018

B. K. Kale
B. K. Kale*
Affiliation:
University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Lehmann [1] in his lecture notes on estimation shows that for estimating the unknown mean of a normal distribution, N(θ, 1), the usual estimator 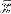is neither minimax nor admissible if it is known that θ belongs to a finite closed interval [a, b] and the loss function is squared error. It is shown that 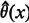, the maximum likelihood estimator (MLE) of θ, has uniformly smaller mean squared error (MSE) than that of 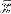. It is natural to ask the question whether the MLE 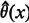of θ in N(θ, 1) is admissible or not if it is known that θ ∊ [a, b]. The answer turns out to be negative and the purpose of this note is to present this result in a slightly generalized form.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 3 , September 1970 , pp. 391 - 393
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Lehmann, E. L., Notes on theory of estimation, Associated Students' Store. Univ. of California, 1949.Google Scholar
2. Lehmann, E. L., Testing statistical hypotheses, Wiley, New York, 1959.Google Scholar
3. Wald, A., Statistical decision functions, Wiley, New York, 1950.Google Scholar