Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T01:11:18.217Z Has data issue: false hasContentIssue false
  • English
  • Français

Inclusion Theorems for the Absolute Summability of Divergent Integrals

Published online by Cambridge University Press:  20 November 2018

Harvey Diamond ,
Brian Kuttner  and
Louise A. Raphael
Harvey Diamond
Affiliation:
Department of Mathematics, West Virginia UniversityMorgantownWest Virginia 26506
Brian Kuttner
Affiliation:
Department of Pure MathematicsThe University of BirminghamBirmingham B15 2TT England
Louise A. Raphael
Affiliation:
Department of Mathematics, Howard UniversityWashingtonD.C. 20059
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Some inclusion theorems are obtained relating the absolute summability of divergent integrals of the form 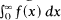under three summability methods: Abelian A(x), Abelian A(lnx) and Stieltjes S(x).

Keywords

40F0540D2540G99
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 26 , Issue 4 , 01 December 1983 , pp. 389 - 398
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Erdelyi, A., Magnus, W., Oberkettinger, F., Tricomi, F. G., Tables of Integral Transforms, Vol. 2 (McGraw Hill, 1954).Google Scholar
2. Hardy, G. H., Divergent Series (Oxford 1949) pp. 73 ff.Google Scholar
3. Knopp, K., Norlund Method for Functions, Math Z, 63 (1955), pp. 39-52.Google Scholar
4. Paley, R. E. A. C. and Wiener, N., Fourier Transforms in the Complex Domain (AMS 1934) pp. 8 ff.Google Scholar
5. Raphael, L. A., The Stieltjes Summability Method and Summing Sturm-Liouville Expansions, SI AM Journal on Mathematical Analysis, 13 (1982), pp. 676-689.Google Scholar
6. Rath, D., An Inclusion Theorem on Summability, J. London Math Soc. (2), 16 (1977), pp. 493-489.Google Scholar
7. Tikhonov, A. N., Stable Methods for the Summation of Fourier Series, Soviet Math. Dokl. 5 (1964), pp. 641-644.Google Scholar
8. Graffi, S., Stieltjes Summability and Convergence of the Fade Approximants for the Vacuum Polarization by an External Field, J. Math. Phys., 14 (1973), pp. 1184-1186.Google Scholar