Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-13T07:21:34.812Z Has data issue: false hasContentIssue false
  • English
  • Français

The Index Theory Associated to a Non-Finite Trace on a C*-Algebra

Published online by Cambridge University Press:  20 November 2018

G. J. Murphy
G. J. Murphy*
Affiliation:
Department of Mathematics, National University of Ireland, Cork, Western Road, Cork, Ireland email: gjm@ucc.ie
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The index theory considered in this paper, a generalisation of the classical Fredholm index theory, is obtained in terms of a non-finite trace on a unital 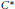${{C}^{*}}$-algebra. We relate it to the index theory of M. Breuer, which is developed in a von Neumann algebra setting, by means of a representation theorem. We show how our new index theory can be used to obtain an index theorem for Toeplitz operators on the compact group 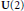$\text{U}\left( 2 \right)$, where the classical index theory does not give any interesting result.

Keywords

46L47B3547L80
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 2 , 01 June 2005 , pp. 251 - 259
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Berger, C. A. and Coburn, L. A., Wiener–Hopf operators on U 2 . J. Integral Equations Operat. Theory 2(1979), 139–173.Google Scholar
[2] Bohr, H., über die Argumentvariation einer fastperiodischen Funktion. Danske Vid. Selsk. 10(1930), 10.Google Scholar
[3] Breuer, M., Fredholm theories in von Neumann algebras I. Math. Ann. 178(1968), 243–254.Google Scholar
[4] Breuer, M., Fredholm theories in von Neumann algebras II. Math. Ann. 180(1969), 313–325.Google Scholar
[5] Coburn, L. A., Douglas, R. G., Schaeffer, D. and Singer, I. M., C*-algebras of operators on a half-space II. Index theory. Inst. Hautes Études Sci. Publ. Math. 40(1971), 69–79.Google Scholar
[6] Connes, A., Noncommutative Geometry. Academic Press, San Diego, 1994.Google Scholar
[7] Dixmier, J., C*-Algebras. North Holland, Amsterdam, 1982.Google Scholar
[8] Murphy, G. J., C*-algebras and Operator Theory. Academic Press, San Diego, 1990.Google Scholar
[9] Murphy, G. J., Toeplitz operators on generalised H 2 spaces. J. Integral Equations Operat. Theory 15(1992), 825–852.Google Scholar
[10] Murphy, G. J., An index theorem for Toeplitz operators. J. Operator Theory 29(1993), 97–114.Google Scholar
[11] Murphy, G. J., Fredholm index and the trace. Proc. Royal Irish Acad. 94(1994), 161–166.Google Scholar
[12] Phillips, J. and Raeburn, I., An index theorem for Toeplitz operators with noncommutative symbol space. J. Funct. Anal. 120(1994), 239–263.Google Scholar
[13] Van Kampen, E., On almost periodic functions of constant absolute value. J. LondonMath. Soc. 12(1937), 3–6.Google Scholar