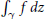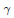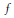Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hua, Liu
2007.
A note about Riemann boundary value problems on non-rectifiable curves.
Complex Variables and Elliptic Equations,
Vol. 52,
Issue. 10-11,
p.
877.
Kats, Boris A.
2012.
Recent Progress in Operator Theory and Its Applications.
p.
137.
Kats, Boris A.
and
Katz, David B.
2016.
Marcinkiewicz exponents and integrals over non‐rectifiable paths.
Mathematical Methods in the Applied Sciences,
Vol. 39,
Issue. 12,
p.
3402.
Kats, Boris A.
and
Katz, David B.
2019.
Curvilinear integrals of discontinuous functions over nonrectifiable paths and Riemann boundary‐value problem.
Mathematical Methods in the Applied Sciences,
Vol. 42,
Issue. 6,
p.
1795.
Katz, David B.
and
Kats, Boris A.
2022.
Torsions and integrations.
Complex Variables and Elliptic Equations,
Vol. 67,
Issue. 7,
p.
1639.
Katz, D. B.
2023.
Generalized Integration over Nonrectifiable Flat Curves and Boundary Value Problems.
Russian Mathematics,
Vol. 67,
Issue. 12,
p.
14.
Katz, D. B.
2023.
Generalized integration over non-recifiable flat curves and boundary value problems.
Izvestiya Vysshikh Uchebnykh Zavedenii. Matematika,
Vol. 1,
Issue. 12,
p.
17.