Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T15:31:11.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinitely Many Rotationally Symmetric Solutions to a Class of Semilinear Laplace–Beltrami Equations on Spheres

Published online by Cambridge University Press:  20 November 2018

Alfonso Castro  and
Emily M. Fischer
Alfonso Castro
Affiliation:
Department of Mathematics, Harvey Mudd College, Claremont, CA 91711, USA e-mail: castro@g.hmc.eduef363@cornell.edu
Emily M. Fischer
Affiliation:
Department of Mathematics, Harvey Mudd College, Claremont, CA 91711, USA e-mail: castro@g.hmc.eduef363@cornell.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that a class of semilinear Laplace–Beltrami equations on the unit sphere in 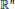${{\mathbb{R}}^{n}}$ has infinitely many rotationally symmetric solutions. The solutions to these equations are the solutions to a two point boundary value problem for a singular ordinary differential equation. We prove the existence of such solutions using energy and phase plane analysis. We derive a Pohozaev-type identity in order to prove that the energy to an associated initial value problem tends to infinity as the energy at the singularity tends to infinity. The nonlinearity is allowed to grow as fast as 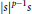${{\left| s \right|}^{p-1}}s$ for 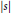$\left| s \right|$ large with 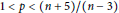$1\,<\,p\,<\,\left( n+5 \right)/\left( n-3 \right)$.

Keywords

58J0535A24Laplace–Beltrami operatorsemilinear equationrotational solutionsuperlinear nonlinearitysub-super critical nonlinearity
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 4 , 01 December 2015 , pp. 723 - 729
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Caicedo, J.E., and Castro, A., Ecuaciones semilineales con espectro discreto. Bogota, Universidad Nacional de Colombia, 2012.Google Scholar
[2] Castro, A., Kwon, J., and Tan, CM. Infinitely many radial solutions for a sub-super critical Dirichlet boundary value problem in a ball. Electron. J. Differential Equations 2007, no. 111.Google Scholar
[3] Castro, A., and Kurepa, A., Infinitely many radially symmetric solutions to a superlinear Dirichlet problem in a ball. Proc. Amer. Math. Soc. 101(1987), no. 1, 57–64. http://dx.doi.Org/10.1090/S0002-9939-1987-0897070-7 Google Scholar
[4] Calzolari, E., Filippucci, R., and Pucci, P., Dead cores and bursts equations for p-Laplacian elliptic equations with weights. In: Discrete and Contin. Dyn. Syst. 2007, Dynamical Systems and Differential Equations. Proceedings of the 6th AIMS International Conference, suppl., 191–200.Google Scholar
[5] Guillemin, V., and Pollack, A., Differential topology. AMS Chelsea Publishing, Providence, RI, 2010.Google Scholar
[6] Jost, J., Riemannian geometry and geometric analysis. Sixth éd., Universitext, Springer, Heidelberg, 2011.Google Scholar
[7] Kristaly, A., Papageorgiou, N. S., and Varga, C., Multiple solutions for a class of Neumann elliptic problems on compact Riemannian manifolds with boundary. Canad. Math. Bull. 53(2010), no. 4, 674–683. http://dx.doi.Org/1 0.41 53/CMB-2O10-073-x Google Scholar
[8] Pohozaev, S. I., Eigenfunctions of the equation Aw + A/(w) = 0. (Russian) Dokl. Akad. Nauk. SSSR 165(1965), 36–39.Google Scholar