Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T14:12:19.820Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinitesimal Hilbertianity of Weighted Riemannian Manifolds

Part of: Global differential geometry Infinite-dimensional manifolds Linear function spaces and their duals

Published online by Cambridge University Press:  27 September 2019

Danka Lučić  and
Enrico Pasqualetto
Danka Lučić
Affiliation:
SISSA, via Bonomea 265, 34136 Trieste, Italy Department of Mathematics and Statistics, P.O. Box 35 (MaD), FI-40014, University of Jyvaskyla, Finland Email: danka.d.lucic@jyu.fienrico.e.pasqualetto@jyu.fi
Enrico Pasqualetto
Affiliation:
SISSA, via Bonomea 265, 34136 Trieste, Italy Department of Mathematics and Statistics, P.O. Box 35 (MaD), FI-40014, University of Jyvaskyla, Finland Email: danka.d.lucic@jyu.fienrico.e.pasqualetto@jyu.fi
Get access Rights & Permissions [Opens in a new window]

Abstract

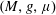The main result of this paper is the following: any weighted Riemannian manifold $(M,g,\unicode[STIX]{x1D707})$, i.e., a Riemannian manifold 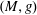$(M,g)$ endowed with a generic non-negative Radon measure 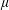$\unicode[STIX]{x1D707}$, is infinitesimally Hilbertian, which means that its associated Sobolev space 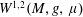$W^{1,2}(M,g,\unicode[STIX]{x1D707})$ is a Hilbert space.

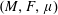We actually prove a stronger result: the abstract tangent module (à la Gigli) associated with any weighted reversible Finsler manifold $(M,F,\unicode[STIX]{x1D707})$ can be isometrically embedded into the space of all measurable sections of the tangent bundle of 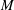$M$ that are 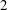$2$-integrable with respect to 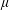$\unicode[STIX]{x1D707}$.

By following the same approach, we also prove that all weighted (sub-Riemannian) Carnot groups are infinitesimally Hilbertian.

Keywords

infinitesimal HilbertianitySobolev spaceFinsler manifoldsmooth approximation of Lipschitz functions

MSC classification

Primary: 53C23: Global geometric and topological methods (à la Gromov); differential geometric analysis on metric spaces
Secondary: 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems 58B20: Riemannian, Finsler and other geometric structures
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 1 , March 2020 , pp. 118 - 140
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akbar-Zadeh, Hassan, Sur les espaces de Finsler á courbures sectionnelles constantes. Acad. Roy. Belg. Bull. Cl. Sci. (5) 74(1988), no. 10, 281–322.Google Scholar
Ambrosio, Luigi, Calculus, heat flow and curvature-dimension bounds in metric measure spaces. In: Proceedings of the ICM 2018. Vol. 1, World Scientific, Singapore, 2019, pp. 301–340. https://doi.org/10.1142/11060Google Scholar
Ambrosio, Luigi, Colombo, Maria, and Di Marino, Simone, Sobolev spaces in metric measure spaces: reflexivity and lower semicontinuity of slope. In: Variational methods for evolving objects. Adv. Stud. Pure Math., 67, Math. Soc. Japan, Tokyo, pp. 1–58. https://doi.org/10.2969/aspm/06710001Google Scholar
Ambrosio, Luigi, Gigli, Nicola, and Savaré, Giuseppe, Gradient flows: in metric spaces and in the space of probability measures. Lectures in Mathematics ETH Zürich, Birkhäuser Verlag, Basel, 2005.Google Scholar
Ambrosio, Luigi, Gigli, Nicola, and Savaré, Giuseppe, Calculus and heat flow in metric measure spaces and applications to spaces with Ricci bounds from below. Invent. Math. 195(2011), no. 2, 289–391. https://doi.org/10.1007/s00222-013-0456-1Google Scholar
Ambrosio, Luigi, Gigli, Nicola, and Savaré, Giuseppe, Density of Lipschitz functions and equivalence of weak gradients in metric measure spaces. Rev. Mat. Iberoamericana. 29(2013), no. 3, 969–996. https://doi.org/10.4171/RMI/746Google Scholar
Ambrosio, Luigi, Gigli, Nicola, and Savaré, Giuseppe, Metric measure spaces with Riemannian Ricci curvature bounded from below. Duke Math. J. 163(2014), 1405–1490. https://doi.org/10.1215/00127094-2681605Google Scholar
Ambrosio, Luigi, Gigli, Nicola, Mondino, Andrea, and Rajala, Tapio, Riemannian Ricci curvature lower bounds in metric measure spaces with 𝜎-finite measure. Transac. Amer. Math. Soc. 367(2015), 4661–4701. https://doi.org/10.1090/S0002-9947-2015-06111-XGoogle Scholar
Azagra, Daniel, Ferrera, Juan, López-Mesas, Fernando, and Rangel, Yenny, Smooth approximation of Lipschitz functions on Riemannian manifolds. J. Math. Anal. Appl. 326(2007), 1370–1378. https://doi.org/10.1016/j.jmaa.2006.03.088Google Scholar
Bao, David Dai-Wai, Chern, Shiing-Shen, and Shen, Zhongmin, An introduction to Riemann-Finsler geometry. Graduate Texts in Mathematics, 200, Springer-Verlag, New York, 2012. https://doi.org/10.1007/978-1-4612-1268-3Google Scholar
Cheeger, Jeff, Differentiability of Lipschitz functions on metric measure spaces. Geom. Funct. Anal. 9(1999), 428–517. https://doi.org/10.1007/s000390050094Google Scholar
Deng, Shaoqiang and Hou, Zixin, The group of isometries of a Finsler space. Pacific J. Math. 207(2002), 149–155. https://doi.org/10.2140/pjm.2002.207.149Google Scholar
Di Marino, Simone, Gigli, Nicola, Pasqualetto, Enrico, and Soultanis, Elefterios, Infinitesimal Hilbertianity of locally $\text{CAT}(\unicode[STIX]{x1D705})$-spaces. Preprint. arxiv:1812.02086Google Scholar
Folland, Gerald B. and Stein, Elias M., Hardy spaces on homogeneous groups. Mathematical Notes, 28, Princeton University Press, Princeton, NJ, 1982.Google Scholar
Garrido, María, Jaramillo, Jesús, and Rangel, Yenny, Smooth approximation of Lipschitz functions on Finsler manifolds. J. Funct. Spaces Appl. 2013 Art. ID 164571. https://doi.org/10.1155/2013/164571Google Scholar
Gigli, Nicola, On the differential structure of metric measure spaces and applications. Mem. Amer. Math. Soc. 236(2015), no. 1113. https://doi.org/10.1090/memo/1113Google Scholar
Gigli, Nicola, Lecture notes on differential calculus on RCD spaces. Publ. Res. Inst. Math. Sci. 54(2018), no. 4, 855–918. https://doi.org/10.4171/PRIMS/54-4-4Google Scholar
Gigli, Nicola, Nonsmooth differential geometry – an approach tailored for spaces with Ricci curvature bounded from below. Mem. Amer. Math. Soc. 21(2018), no. 1196. https://doi.org/10.1090/memo/1196Google Scholar
Gigli, Nicola and Pasqualetto, Enrico, Behaviour of the reference measure on RCD spaces under charts. Commun. Anal. Geom. to appear. arxiv:1607.05188Google Scholar
Gigli, Nicola, Pasqualetto, Enrico, and Soultanis, Elefterios, Differential of metric valued Sobolev maps. Journal of Functional Analysis. to appear. arxiv:1807.10063Google Scholar
Heinonen, Juha, Koskela, Pekka, Shanmugalingam, Nageswari, and Tyson, Jeremy T., Sobolev spaces on metric measure spaces. An approach based on upper gradients. New Mathematical Monographs, 27, Cambridge University Press, Cambridge, 2015. https://doi.org/10.1017/CBO9781316135914Google Scholar
Jiménez-Sevilla, Mar and Sánchez-González, Luis, On some problems on smooth approximation and smooth extension of Lipschitz functions on Banach-Finsler manifolds. Nonlinear Anal. 74(2011), 3487–3500. https://doi.org/10.1016/j.na.2011.03.004Google Scholar
Le Donne, Enrico, A primer on Carnot groups: homogeneous groups, Carnot-Carathéodory spaces, and regularity of their isometries. Anal. Geom. Metr. Spaces 5(2017), no. 1, 116–137. https://doi.org/10.1515/agms-2017-0007Google Scholar
Lott, John and Villani, Cédric, Weak curvature conditions and functional inequalities. J. Funct. Anal. 245(2007), 311–333. https://doi.org/10.1016/j.jfa.2006.10.018Google Scholar
Lučić, Danka and Pasqualetto, Enrico, The Serre-Swan theorem for normed modules. Rendiconti del Circolo Matematico di Palermo Series 2 68(2019), 385–402. https://doi.org/10.1007/s12215-018-0366-6Google Scholar
Shanmugalingam, Nageswari, Newtonian spaces: an extension of Sobolev spaces to metric measure spaces. Rev. Mat. Iberoamericana 16(2000), 243–279. https://doi.org/10.4171/RMI/275Google Scholar
Sturm, Karl-Theodor, On the geometry of metric measure spaces. I. Acta Math. 196(2006), 65–131. https://doi.org/10.1007/s11511-006-0002-8Google Scholar
Sturm, Karl-Theodor, On the geometry of metric measure spaces. II. Acta Math. 196(2006), 133–177. https://doi.org/10.1007/s11511-006-0003-7Google Scholar
Villani, Cédric, Synthetic theory of Ricci curvature bounds. Jpn. J. Math. 11(2016), 219–263. https://doi.org/10.1007/s11537-016-1531-3Google Scholar
Villani, Cédric, Inégalités isopérimétriques dans les espaces métriques mesurés. Séminaire Bourbaki, bourbaki.ens.fr/TEXTES/1127.pdfGoogle Scholar