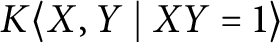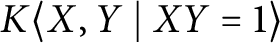Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Abrams, Gene
Mantese, Francesca
and
Tonolo, Alberto
2024.
Injectives over Leavitt path algebras of graphs with disjoint cycles.
Journal of Pure and Applied Algebra,
Vol. 228,
Issue. 7,
p.
107646.