No CrossRef data available.
Article contents
Injectivity of the Connecting Homomorphisms in Inductive Limits of Elliott–Thomsen Algebras
Part of:
Selfadjoint operator algebras
Published online by Cambridge University Press: 07 January 2019
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let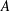 
$A$ be the inductive limit of a sequence with 
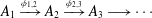$$\begin{eqnarray}A_{1}\xrightarrow[{}]{\unicode[STIX]{x1D719}_{1,2}}A_{2}\xrightarrow[{}]{\unicode[STIX]{x1D719}_{2,3}}A_{3}\longrightarrow \cdots\end{eqnarray}$$
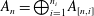$A_{n}=\bigoplus _{i=1}^{n_{i}}A_{[n,i]}$, where all the 
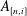$A_{[n,i]}$ are Elliott–Thomsen algebras and 
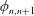$\unicode[STIX]{x1D719}_{n,n+1}$ are homomorphisms. In this paper, we will prove that 
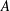$A$ can be written as another inductive limit with 
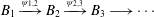$$\begin{eqnarray}B_{1}\xrightarrow[{}]{\unicode[STIX]{x1D713}_{1,2}}B_{2}\xrightarrow[{}]{\unicode[STIX]{x1D713}_{2,3}}B_{3}\longrightarrow \cdots\end{eqnarray}$$
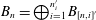$B_{n}=\bigoplus _{i=1}^{n_{i}^{\prime }}B_{[n,i]^{\prime }}$, where all the 
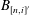$B_{[n,i]^{\prime }}$ are Elliott–Thomsen algebras and with the extra condition that all the 
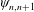$\unicode[STIX]{x1D713}_{n,n+1}$ are injective.
MSC classification
Secondary:
46L35: Classifications of $C^*$-algebras
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
References
Blackadar, B., Bratteli, O., Elliott, G. A., and Kumjian, A.,
Reduction of real rank in inductive limits of C
∗-algebras
. Math. Ann.
292(1992), 111–126. https://doi.org/10.1007/BF01444612.Google Scholar
Elliott, G. A.,
A classification of certain simple C
∗-lgebras
. In: Quantum and non-commutative analysis (Kyoto, 1992), Math. Phys. Stud., 16, Kluwer Acad. Publ., Dordrecht, 1993, pp. 373–385.Google Scholar
Elliott, G. A.,
On the classification of C
∗-algebras of real rank zero
. J. Reine. Angew. Math.
443(1993), 179–219. https://doi.org/10.1515/crll.1993.443.179.Google Scholar
Elliott, G. A.,
A classification of certain simple C
∗-algebras, II
. J. Ramanujan Math. Soc.
12(1997), 97–134.Google Scholar
Elliott, G. A., Gong, G., and Li, L.,
Injectivity of the connecting maps in AH inductive systems
. Canad. Math. Bull.
48(2005), 50–68. https://doi.org/10.4153/CMB-2005-005-9.Google Scholar
Eliott, G. A. and Thomsen, K.,
The state space of the K
0-group of a simple separable C
∗-algebra
. Geom. Funct. Anal.
4(1994), 522–538. https://doi.org/10.1007/BF01896406.Google Scholar
Gong, G.,
On the classification of simple inductive limit C
∗-algebras, I. The reduction theorem
. Doc. Math.
7(2002), 255–461.Google Scholar
Gong, G. and Lin, H., On classification of simple non-unital amenable C
∗-algebras, II. arxiv:1702.01073.Google Scholar
Gong, G., Lin, H., and Niu, Z., Classification of finite simple amenable
${\mathcal{Z}}$
-stable C
∗-algebras. arxiv:1501.00135v6.Google Scholar
${\mathcal{Z}}$
-stable C
∗-algebras. arxiv:1501.00135v6.Google ScholarLi, L.,
Classification of simple C
∗-algebras inductive limits of matrix algebras over trees
. Mem. Amer. Math. Soc.
127(1997), no. 605.Google Scholar
Li, L.,
Simple inductive limit C
∗-algebras: Spectra and approximation by interval algebras
. J. Reine Angew. Math.
507(1999), 57–79. https://doi.org/10.1515/crll.1999.019.Google Scholar
Li, L.,
Classification of simple C
∗-algebras: inductive limit of matrix algebras over 1-dimensional spaces
. J. Funct. Anal.
192(2002), 1–51. https://doi.org/10.1006/jfan.2002.3895.Google Scholar
Liu, Z., A decomposition theorem for real rank zero inductive limits of 1-dimensional non-commutative CW complexes. arxiv:1709.03684v1.Google Scholar
Su, H.,
On the classification of C
∗-algebras of real rank zero: Inductive limits of matrix algebras over non-Hausdorff graphs
. Mem. Amer. Math. Soc.
114(1995), no. 547. https://doi.org/10.1090/memo/0547.Google Scholar
You have
Access