Article contents
Involutions and Anticommutativity in Group Rings
Published online by Cambridge University Press: 20 November 2018
Abstract
Let  $g\,\mapsto \,{{g}^{*}}$ denote an involution on a group
$g\,\mapsto \,{{g}^{*}}$ denote an involution on a group  $G$. For any (commutative, associative) ring
$G$. For any (commutative, associative) ring  $R$ (with 1),
$R$ (with 1),  $*$ extends linearly to an involution of the group ring
$*$ extends linearly to an involution of the group ring 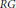 $RG$. An element
$RG$. An element 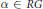 $\alpha \,\in \,RG$ is symmetric if
$\alpha \,\in \,RG$ is symmetric if 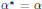 ${{\alpha }^{*}}\,=\,\alpha $ and skew-symmetric if
${{\alpha }^{*}}\,=\,\alpha $ and skew-symmetric if 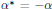 ${{\alpha }^{*}}\,=\,-\alpha $. The skew-symmetric elements are closed under the Lie bracket,
${{\alpha }^{*}}\,=\,-\alpha $. The skew-symmetric elements are closed under the Lie bracket, 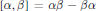 $[\alpha ,\,\beta ]\,=\,\alpha \beta \,-\,\beta \alpha $. In this paper, we investigate when this set is also closed under the ring product in
$[\alpha ,\,\beta ]\,=\,\alpha \beta \,-\,\beta \alpha $. In this paper, we investigate when this set is also closed under the ring product in 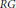 $RG$. The symmetric elements are closed under the Jordan product,
$RG$. The symmetric elements are closed under the Jordan product, 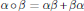 $\alpha \,o\,\beta \,=\,\alpha \beta \,+\beta \alpha $. Here, we determine when this product is trivial. These two problems are analogues of problems about the skew-symmetric and symmetric elements in group rings that have received a lot of attention.
$\alpha \,o\,\beta \,=\,\alpha \beta \,+\beta \alpha $. Here, we determine when this product is trivial. These two problems are analogues of problems about the skew-symmetric and symmetric elements in group rings that have received a lot of attention.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013
References
- 3
- Cited by


